Множественная (многофакторная) регрессия
Изучение связи между тремя и более связанными между собой признаками носит название множественной регрессии. Задача состоит в определении аналитического выражения связи между результативным признаком (у) и факторным признаками (х1,х2,х3…хn).
Построение моделей множественной регрессии включает несколько этапов: - выбор формы связи (уравнение регрессии) - отбор факторных признаков - обеспечение достаточного объема совокупности для получения несмещенных оценок. Рассмотрим каждый из них: 1. Выбор формы связи. Наиболее применимый способ – это метод перебора различных уравнений. Сущность метода заключается в том, что большое число уравнений, отобранных для описания связи какого-либо социально-экономического явления или процесса, реализованного на ЭВМ с помощью специально разработанных программ перебора с последующей статистической проверкой на основе t-критерия Стьюдента и F-критерия Фехнера – Снедекора. Этот способ очень трудоемкий. Практика построения многофакторных моделей показывает, что все реально существующие зависимости между социально-экономическими явлениями можно описать 5 типами моделей.
1. Линейная
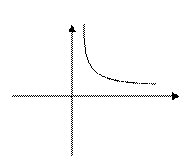
2. Степенная
3. Показательная
4. Параболическая
5. Гиперболическая
Основное значение имеют линейные модели в силу своей простоты и логичности их экономической интерпретации. Нелинейные формы зависимости приводятся к линейным путем линеаризации. 2. Отбор факторных признаков. Сложность формирования уравнения множественной регрессии заключается в том, что почти все факторные признаки находятся в зависимости один от другого. Вторая проблема определения оптимального числа факторных признаков. С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью меньше 100 факторов сложно реализуема и требует больших затрат машинного времени. Т.е. необходимо исключить второстепенные, экономически и статистически несущественные факторы. И слишком малая модель будет недостаточно адекватно исследуемым явлениям. Модель может осуществляться следующими методами: а) Экспертных оценок основан на интуитивно – логических предпосылках, содержательно-качественном анализе. Анализ экспертной информации проводится на базе расчета и анализа непараметрических показателей связи: ранговых коэффициентов корреляции Спирмэна, Кендела и Конкордации. Ранг – это порядковый номер значения признака, располож. в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным среднему арифметическому от соответствующего номера лист., который определяют. Такие ранги называют связными. Пример. Проранжировать предприятия автомобильной промышленности одного из регионов по величине балансовой прибыли.
б) Наиболее применимы – шаговая регрессия. Сущность метода заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Факторы поочередно вводятся в уравнение так называемым «прямым методом». При проверке значимости введенного фактора определяется насколько уменьшается сумма квадратов оcтатков и увеличивается величина множественного коэффициента корреляции (R).
где δ2 – дисперсия теоретического значения результативного признака, рассчитанного по уравнению множественной регрессии.
σ2 – общая дисперсия результативного признака. 0≤R≤1 Приближаясь к 1 он свидетельствует о силе зависимости между признаками. При небольшом числе наблюдений величина коэффициента R, как правило завышается. Однако используется и обратный метод, т.е. исключение факторов, ставших незначительными на основе t-критерия Стьюдента. Фактор является незначительным, если он вкл. в уравнение регрессии только изменяет значение коэффициента регрессии, не уменьшая сумму квадратов остатков и не увеличивая их значения. Если при вкл. в модель соответствующего факторного признака величина множественного коэффициента регрессии не изменяется (или меняется несущественно), то данный признак существенен и его вкл. в уравнение регрессии необходимо. Если же при вкл. в модель факторного признака коэффициент регрессии меняют не только величину, но и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак признается нецелесообразным для включения в модель связи. Качество уравнения регрессии зависит от степени. Параметры уравнения множественной регрессии показывают степень влияния каждого фактора на анализируемый показатель при фиксированном (среднем) значении всех других факторов.
|

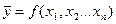
 1,2…n=a0+a1x1+a2x2+…+anxn
1,2…n=a0+a1x1+a2x2+…+anxn







 - остаточная дисперсия
- остаточная дисперсия


