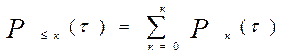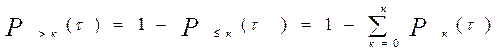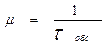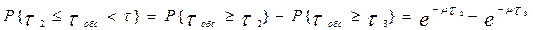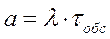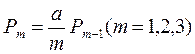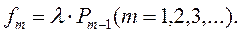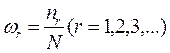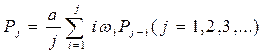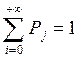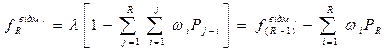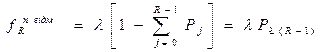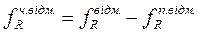Завдання № 1. 1) Моделювання потоку викликів оперативно-рятувальних підрозділів в місті.1) Моделювання потоку викликів оперативно-рятувальних підрозділів в місті. Кількість викликів «N» за якими оперативно-рятувальні підрозділи виїжджали протягом часу t=1 рік, визначається по початкових даних:
N =n1+n2+n3+n4
Послідовність випадкових моментів викликів оперативно-рятувальних підрозділів в місті створює потік подій, що має важливу характеристику інтенсивності потоку «λ» (щільність потоку) за одиницю часу:
Математичною моделлю потоку подій, що описує розподілення імовірностей виникнення тої чи іншої кількості подій на інтервалі часу визначеної довжини, є закон розподілення Пуассона. Згідно до цього закону імовірність Рк(t) того, що на інтервалі часу протягом «t» виникне рівно «R» подій, визначається за формулою:
При використанні даної формули розмірності одиниць вимірювання часу «l» і «t» повинні бути погоджені. Імовірності Рк(t1) (к = 0, 1, 2,...) для інтервалу часу фіксованого періоду «t», пов’язані між собою співвідношенням:
З цієї формули випливає: імовірності того, що на інтервалі часу «t» виникає кількість подій, яка не перевищує задане число «К» і перевищує число «К», пов'язані між собою співвідношенням:
визначаються за формулами:
2) Моделювання тривалості часу зайнятості оперативно-рятувальних підрозділів обслуговуванням викликів в місті. При здійсненні опису імовірності розподілення випадкової величини tобс тривалості часу зайнятості оперативно-рятувальних підрозділів обслуговуванням викликів за допомогою показового закону розподілення необхідно визначити значення параметру «μ» (інтенсивність потоку «звільнень» підрозділів від обслуговування викликів):
Імовірність того, що тривалість часу зайнятості підрозділів обслуговуванням виклику tобс буде менша або більша від даного значення «t» знаходять за формулами:
Р{ t обс< t2 }=1-е-μt2 Р{ t обс≥;t3 }=1- Р{ t обс≥;t3 }=е-μt3
Імовірність знаходження значення випадкової величини tобс в заданих межах t 2 ≤tобс<t3 визначається за формулою:
Розмірності величин μ та t повинні бути погоджені
3) Математичне моделювання процесу виникнення одночасних викликів оперативно-рятувальних підрозділів в місті. Можливий стан оперативно-рятувальних підрозділів міста позначаємо Е0, Е1, Ез, … - пронумеруємо за кількістю викликів, обслуговуванням яких зайняті підрозділи. В довільний момент часу підрозділи міста можуть знаходитися лише в одному стані Еm (m=0, 1, 2,...). Можливі переходи із стану Еm до стану Еm-1 у випадку «звільнення» підрозділів від обслуговування одного з m викликів, або до стану Еm+1, якщо виникає ще один виклик. Процес виникнення одночасних викликів має випадковий характер і йому властиві імовірні закономірності. Імовірність Рm того, що в довільний момент часу підрозділи знаходяться у стані Еm одночасного обслуговування m викликів, визначається за формулою:
Де а - приведена щільність потоку викликів.
Розмірність одиниць вимірювання за часом повинна бути погоджена. З метою послідовних визначень імовірності Р0, Р1, P2, … використовують рекурентні формули:
Число fm випадків, що очікуються на протязі одиничного відрізка часу, коли при виникненні чергового виклику виникає необхідність в одночасному обслуговуванні того чи іншого числа m викликів визначається за формулою:
Між значеннями Рm та fm мають місце наступні співвідношення, які можуть бути використані для перевірки правильності розрахунків:
4) Математичне моделювання процесу зайнятості оперативно-рятувальних підрозділів обслуговуванням викликів. Заздалегідь невідома кількість відділень оперативно-рятувальних підрозділів, що буде виїжджати на кожен виклик. Імовірність ωr того, що для обслуговування виклику необхідно залучати r оперативних відділень, визначається за підсумками статистичних даних про виклики підрозділів таким чином:
Кількість оперативних відділень, що задіяні в обслуговуванні викликів j, змінюється з часом, і процес її зміни може розглядатися як випадковий. Імовірність Рj того, що в довільний момент часу на обслуговуванні виклику в місті буде одночасно задіяно j відділень, розраховується за допомогою рекурентної формули:
де: Імовірності Рj (j=0, 1, 2,...) пов'язані між собою співвідношенням:
В місті діє «R» оперативних відділень оперативно-рятувальних підрозділів. Для кожного значення R=0, 1, 2, 3, 4 можна дати оцінку імовірності Р>R того, що кількості «R» відділень буде недостатньо для обслуговування викликів у місті, буде потрібна кількість відділень, що перевищує значення «R», і ці відділення доведеться залучати ззовні міста:
Коли немає можливості виїзду по черговому виклику достатньої кількості відділень, виникає стан, який називається відмовою. Відмова може бути повною, якщо немає можливості на виїзд жодного відділення. Відмова може бути частковою, коли по виклику можуть виїхати відділення у такій кількості, яка менша за потрібну для його обслуговування. При заданій кількості «R» відділень в місті загальна кількість відмов ƒвідм.R, що очікується протягом одиничного відрізку часу, а також кількість повних відмов ƒп.відм..R і кількість часткових відмов ƒч.відм..R в обслуговуванні викликів визначаються за формулами:
При цьому ставиться на меті забезпечення можливості оперативно-рятувальних підрозділів міста обслуговувати виклики без залучення додаткових відділень ззовні міста. Це досягається шляхом збільшення кількості відділень R і визначається в низьких значеннях величин ƒвідм.R, ƒп.відм..R і ƒч.відм..R. З економічних міркувань можна обмежитися кількістю відділень, яка б дозволяла не дуже часто відволікати додаткові відділення від несення бойового чергування в своїх районах обслуговування.
|
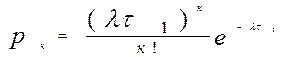(К=0, 1, 2, 3…)
