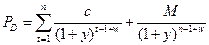Вычисление доходности к сроку погашения в случае, если расчетный день происходит между купонными платежами
В прошлой главе мы показали, как определить цену, которую платит продавец, когда облигация покупается между купонными платежами. Выплаченная сумма в таком случае – полная, «грязная» цена, цена облигации с учетом наросших процентов. Доходность к сроку погашения для облигации, когда расчетный день выпадает между купонными выплатами – это ставка процента, которая сделает приведенную стоимость денежных потоков равной полной, «грязной» цене. Для полугодовой облигации с n оставшимися купонными выплатами это значит решить уравнение относительно y:
где PD – «грязная» цена облигации, ден. ед.; с – полугодовые купонные платежи, ден. ед.; у – половина показателя доходности к сроку погашения облигации, доли ед. n –количество оставшихся купонных платежей; М – цена погашения облигации, ден. ед. w – определяется как отношение количества дней между сделкой и днем следующего купонного платежа (TS) к количеству дней в купонном периоде (Tcp), то есть: w = TS / Tcp.
Удвоение величины y дает доходность к сроку погашения в расчете на год. Можно иначе написать:
|

 (5.3)
(5.3)