Пример 5.3.
В примере 5.1 мы вычисляли текущую доходность для 18-ти летней облигации с 6% купонной ставкой, продаваемой по 70 089 руб. Купонные платежи осуществляются дважды в год. Номинальная стоимость облигации – 100 000 руб. Требуется определить доходность к сроку погашения облигации. Денежные потоки, генерируемые облигацией: 1) 36 купонных выплат по 3 000 руб. каждые 6 месяцев; 2) 100 000 руб. через 36 месяцев. Для вычисления y, нужно перебрать различные процентные ставки, пока одна из них не сделает текущую стоимость денежных потоков, равной 70 089 руб. При этом следует отметить, что купонная ставка облигации равна 6% и облигация продается с дисконтом, следовательно, доходность должна быть больше 6%. Рассмотрим различные полугодовые ставки процента от 3,25% до 4,75% (соответствующие годовым ставкам процента от 6,50% до 9,50% соответственно), которые выбираются в качестве ставки дисконтирования.
При этом приведенная стоимость 36 выплат по 3 000 руб. вычисляется с помощью аннуитета:
приведенная стоимость 100 000 руб. (номинальной стоимости облигации):
Подставляя в приведенные выше формулы ставки дисконтирования от 3,25 % до 4,75%, мы находим тот показатель дисконтирования, который обеспечивает равенство цены облигации приведенной стоимости всех денежных потоков, генерируемых этой облигацией. Как видно из приведенных вычислений, ставка 4,75% дает приведенную стоимость денежных потоков в 70 089 руб. Поэтому y = 4,75%, а доходность к сроку погашения составляет 9,5 % в год.
|

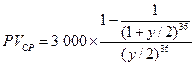 ,
,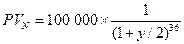 .
.


