Типовые дискретные сигналы
При исследовании линейных дискретных систем ряд дискретных сигналов используют в качестве испытательных воздействий; такие сигналы называют типовыми. К ним относятся: Цифровой единичный импульс, описываемый последовательностью
из чего следует, что этот сигнал равен единице при
Рис. 1.2. Цифровой единичный импульс Задержанный цифровой единичный импульс, описываемый последовательностью
из чего следует, что этот сигнал, в отличие от незадержанного, равен единице только при Произвольный дискретный сигнал можно описать в виде суммы
что оказывается удобным при выводе ряда соотношений (см п. 1.3.1). Подставляя в (1.5) любое значение
откуда, с учетом определения цифрового единичного импульса
Дискретная экспонента, описываемая последовательностью
Рис. 1.3. Дискретная экспонента Вид дискретной экспоненты определяется величиной и знаком параметра при при при при при Дискретный гармонический сигнал (дискретная косинусоида или синусоида); например, дискретная косинусоида, описываемая последовательностью
где T – период дискретизации, A – амплитуда, w = 2p – круговая частота. Дискретная косинусоида получается из аналоговой
в результате замены непрерывного времени дискретным (рис. 1.4)
Рис. 1.4. Дискретная косинусоида Дискретная синусоида описывается аналогично. Дискретный комплексный гармонический сигнал, описываемый комплексной последовательностью
или, при разложении по формуле Эйлера, двумя вещественными последовательностями – косинусоидой (вещественная часть) и синусоидой (мнимая часть)
|

 (1.3)
(1.3)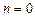 и нулю при всех остальных значениях
и нулю при всех остальных значениях 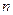 (рис.1.2, а).
(рис.1.2, а).
 (1.4)
(1.4)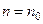 и нулю при всех остальных значениях
и нулю при всех остальных значениях  , (1.5)
, (1.5) при
при  имеем
имеем ,
, (1.3), имеем
(1.3), имеем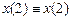 .
. (1.6)
(1.6)
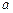 , а именно:
, а именно: и
и  дискретная экспонента будет убывающей, знакопостоянной (рис. 1.3, а);
дискретная экспонента будет убывающей, знакопостоянной (рис. 1.3, а);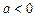 – убывающей, знакопеременной (рис. 1.3, б);
– убывающей, знакопеременной (рис. 1.3, б);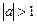 – возрастающей;
– возрастающей; и
и 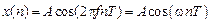 , (1.7)
, (1.7)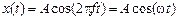
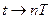 .
.
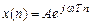 ,
, .
.


