Разностное уравнение
Взаимосвязь между воздействием
где
i, k – значения задержек воздействия и реакции соответственно; N, M – константы;
Коэффициенты Для нормированного времени разностное уравнение (1.14) принимает вид
Линейная дискретная система, соотношение вход/выход которой описывается в виде разностного уравнения (1.15), отвечает условиям физической реализуемости: принулевыхначальныхусловиях (1.9) реакция не может возникнуть раньше воздействия; значения реакции в каждый момент времени Разностное уравнение (1.15) решается методом прямой подстановки при нулевых начальных условиях (1.9), следовательно, оно непосредственно описывает алгоритм вычисления реакции по известному воздействию и параметрам ЛДС. Пример 1.2. Решить разностное уравнение
методом прямой подстановки при заданном воздействии и нулевых начальных условиях
Требуется определить 5 отсчетов реакции. Решение приведено в табл. 1.2. Таблица 1.2
|
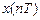и реакцией 
– соотношение вход/выход – может описываться разностным уравнением (РУ)
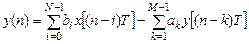, (1.14)
, 
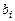– коэффициенты уравнения (вещественные константы);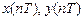
– воздействие и реакция (вещественные или комплексные сигналы);
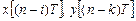– воздействие и реакция, задержанные на i и k периодов дискретизации соответственно.
. (1.15)
зависят только от текущего и предшествующих значений воздействия, но не зависят от его последующих значений (см. п. 1.3).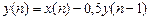
.
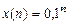