ВВЕДЕНИЕ. Цифровая обработка сигналов (ЦОС) – это область науки и техники, в которой изучаются общие для разных дисциплин алгоритмы и средства обработки сигналов
Цифровая обработка сигналов (ЦОС) – это область науки и техники, в которой изучаются общие для разных дисциплин алгоритмы и средства обработки сигналов средствами цифровой вычислительной техники. Программа дисциплины «Цифровая обработка сигналов» на заочном отделении включает следующие основные темы. Тема 1. Введение в ЦОС Основные типы сигналов. Типовые дискретные сигналы. Нормирование частоты. Обобщенная система ЦОС. Z -преобразование. Тема 2. Линейные дискретные системы (ЛДС) Математическое описание ЛДС во временной области: импульсная характеристика; соотношение вход/выход; формула свертки; разностное уравнение; рекурсивные и нерекурсивные ЛДС; КИХ- и БИХ-системы; определение и критерий устойчивости. Математическое описание ЛДС в z -области: передаточная функция; соотношение вход/выход; взаимосвязь передаточной функции с разностным уравнением и импульсной характеристикой; карта нулей и полюсов; оценка устойчивости по передаточной функции. Математическое описание ЛДС в частотной области: частотная характеристика; соотношение вход/выход; свойства частотной характеристики, ее расчет и анализ. Тема 3. Дискретные сигналы Спектр дискретного сигнала и его свойства; связь между спектрами дискретного и аналогового сигналов; дискретное преобразование Фурье (ДПФ); быстрое преобразование Фурье (БПФ). Тема 4. Введение в цифровые фильтры (ЦФ) Определение и классификация; основные этапы синтеза ЦФ; задание требований к АЧХ и характеристике ослабления; КИХ-фильтры с линейной ФЧХ. Тема 5. Синтез ЦФ Синтез оптимальных (по Чебышеву) КИХ-фильтров; синтез БИХ-фильтров методом билинейного Z -преобразования. Тема 6. Квантование в цифровых системах Источники шумов в цифровых системах; предположение об источниках; детерминированные и вероятностные оценки шумов квантования; эффекты переполнения в сумматорах; понятие о предельных циклах. Тема 7. Реализация алгоритмов ЦОС Понятие о реальном времени алгоритмов ЦОС и их программной реализации на базе процессоров цифровой обработки сигналов (ЦПОС); краткий обзор особенностей архитектуры ЦПОС ведущих на российском рынке фирм-производителей. Данное учебное пособие посвящено изучению темы 2 и разработано на базе курса лекций [1], который рекомендуется в качестве основного по дисциплине «Цифровая обработка сигналов». Учебное пособие включает 3 раздела: 1. Теоретические основы линейных дискретных систем. 2. Задание на контрольную работу. 3. Типовые примеры выполнения контрольной работы. Приводится список литературы и предметный указатель. 1. ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ: В этом разделе дается краткая теоретическая справка по анализу линейных дискретных систем и приводится необходимый сопутствующий материал. 1.1. Аналоговые и дискретные сигналы. Сигналом называют физический процесс, несущий в себе информацию. Математически сигналы описываются функциями времени, тип которых зависит от типа сигнала. К основным типам сигналов относят: аналоговый, дискретный, цифровой. Аналоговым называется сигнал, непрерывный во времени и по состоянию (рис. 1.1, а). Такой сигнал описывается непрерывной (или кусочно-непрерывной) функцией Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию (рис. 1.1, б). Он описывается решетчатой функцией (последовательностью) x (nT), где n = 0, 1, 2, … Последовательность x (nT) определена только в моменты времени nT и может принимать любые значения из некоторого интервала Комплексный дискретный сигнал описывается двумя вещественными последовательностями Цифровым называют сигнал, дискретный по времени и квантованный по состоянию. Такой сигнал описывается квантованной решетчатой функцией (квантованной последовательностью Интервал
– частотой дискретизации.
Рис. 1.1. Примеры аналогового и дискретного сигналов При анализе дискретных сигналов удобно пользоваться нормированным временем
откуда при
Таким образом, номер n отсчета дискретного сигнала является нормированным временем: иначе говоря, номер n означает, что отсчет взят в момент nT. Переход к нормированному времени позволяет рассматривать дискретный сигнал как функцию целочисленной переменной В дальнейшем обозначения дискретного сигнала
|

 , причем и аргумент, и сама функция могут принимать любые значения из некоторых интервалов
, причем и аргумент, и сама функция могут принимать любые значения из некоторых интервалов  ,
,  соответственно.
соответственно. .
.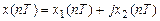 .
.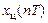 ), отсчеты которой в каждый момент времени
), отсчеты которой в каждый момент времени 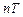 принимают квантованные значения из некоторого интервала
принимают квантованные значения из некоторого интервала  .
.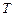 называют периодом дискретизации, а обратную величину
называют периодом дискретизации, а обратную величину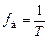 (1.1)
(1.1)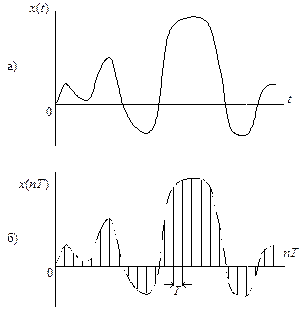
 ,
,
 . (1.2)
. (1.2)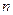 .
. и
и 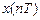 будем считать тождественными
будем считать тождественными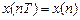 .
.


