Погрешности арифметических операций
Приведем правила вычисления погрешности результата различных арифметических операций над приближенными числами.
Относительно алгебраической суммы u = х ± у можно утверждать следующее.
Теорема 1.2. Предельная абсолютная погрешность суммы приближенных чисел равна сумме предельных абсолютных погрешностей слагаемых, т. е.
Δu = Δx + Δy (1.13)
Из формулы (1.13) следует, что предельная абсолютная погрешность суммы не может быть меньше предельной абсолютной погрешности наименее точного из слагаемых, т. е. если в состав суммы входят приближенные слагаемые с разными абсолютными погрешностями, то сохранять лишние значащие цифры в более точных не имеет смысла.
Пример 1.12. Найти сумму приближенных чисел, все цифры которых являются верными в широком смысле, и ее предельную абсолютную и относительную погрешности u= 0.259 + 45.12+ 1.0012. Решение. Предельные абсолютные погрешности слагаемых здесь равны соответственно 0.001; 0.01; 0.0001. Суммирование производим, руководствуясь следующим правилом:
1) выделим наименее точные слагаемые (в нашем примере это второе слагаемое) и оставим их без изменения;,
2) остальные числа округлим по образцу выделенных, оставляя один или два запасных знака;
3) сложим данные числа, учитывая все сохраненные знаки;
4)полученный результат округлим до точности наименее точных слагаемых. Имеем Δu = 0.001 + 0.01 + 0.0001 = 0.0111; u = 0.259 + 45.12 + 1.0012 = 0.26 + 45.12 + 1.00 = 46.38 ± 0.01.
Основной вклад в абсолютную погрешность результата здесь вносят предельные погрешности исходных данных, приведенные выше.
Теорема 1.3. Если все слагаемые в сумме имеют один и тот же знак, то предельная относительная погрешность суммы не превышает наибольшей из предельных относительных погрешностей слагаемых:
При вычислении разности двух приближенных чисел u = х - у ее абсолютная погрешность, согласно теореме 1.2, равна сумме абсолютных погрешностей уменьшаемого и вычитаемого, т. е. Δu = Δx + Δy, а предельная относительная погрешность
Из формулы (1.15) следует, что если приближенные значения х и у близки, то предельная относительная погрешность будет очень большой.
Пример 1.13. Найти разность х - у с тремя верными знаками, если х = 12.1254 ± 0.0001, у = 12.128 ± 0.001.
|

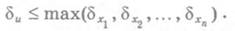 (1.14)
(1.14)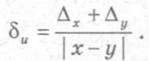 (1.15)
(1.15)


