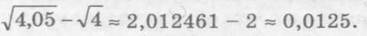Решение. Согласно этим результатам разность х - у имеет не более одной верной цифры и относительная погрешность очень велика по
Имеем 12.1254 – 12.128 = - 0.0026. Δu = 0.0001 + 0.001 = 0.0011; δu= 0.0011/|-0.00261 =0.42; δx =0.0001/ 12.1254 = 0.000008; δy =0.001 /12.128 = 0.00008.
Согласно этим результатам разность х - у имеет не более одной верной цифры и относительная погрешность очень велика по сравнению с относительными погрешностями операндов. В некоторых случаях удается избежать вычисления разности близких чисел с помощью преобразования выражения так, чтобы разность была исключена. Рассмотрим один из таких примеров.
Пример 1.14. Найти разность
Решение. Умножим и разделим на сумму. Получим
Если представляется сложным заменить вычитание близких приближенных чисел сложением, то следует поступать так: если известно, что при вычитании должно пропасть m первых значащих цифр, а в результате требуется сохранить n верных цифр, тогда в уменьшаемом и вычитаемом следует сохранять m + n верных зна чащих цифр:
Теорема 1.4. Предельная относительная погрешность произведения u = х ∙у приближенных чисел, отличных от нуля, равна сумме предельных относительных погрешностей сомножителей, т. е. δu = δx + δy. (1.16) В частности, если u = kx, где k — точное число, имеем Δu = |k| Δx, δu = δx.
Пример 1.15. Определить произведение приближенных чисел х = 12.45 и у = 2.13 и число верных значащих цифр в нем, если все написанные цифры сомножителей — верные в узком смысле.
|

 с тремя верными знаками.
с тремя верными знаками.