МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ПОГРЕШНОСТИ

Практические и лабораторные занятия

ТЕМА № 1

МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ПОГРЕШНОСТИ

 

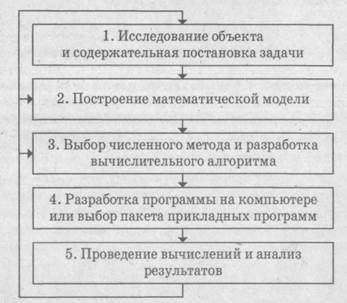
Процесс решения задачи из физики, техники или экономики с помощью методов математического моделирования состоит из нескольких этапов (рис. 1.1).

 

 

Рис. 1.1. Процесс решения задачи

 

1. На первом этапе проводится исследование объекта и формулируется содержательная (физическая, техническая, экономическая и др.) постановка задачи. Для того чтобы задачу можно было описать количественно, нужно провести качественный и количественный анализ свойств объекта и выделить основные параметры, оказывающие на них наиболее существенное влияние.

 

2. Следующим этапом является математическая постановка задачи, в процессе которой осуществляется построение математической модели объекта. Под математической моделью понимают систему математических соотношений (уравнений, неравенств, краевых, начальных условий), которым должна удовлетворять система основных параметров задачи или объекта. Одно из основных требований, предъявляемых к математической модели, — соответствие исследуемому объекту, т. е. адекватность. Другое немаловажное требование— чтобы модель была не слишком сложной, доступной для математической обработки. Умение находить оптимальное сочетание адекватности и сложности зависит от квалификации и даже интуиции исследователя и является в определенной степени искусством.

 

3. На следующем этапе необходимо найти методы (алгоритмы) решения математической задачи. В некоторых, наиболее простых случаях удается построить аналитическое решение задачи. Такие решения являются наиболее привлекательными, поскольку позволяют не только количественно, но и, что не менее важно, качественно проанализировать исследуемые параметры. К сожалению, в подавляющем большинстве случаев это не представляется возможным, и для решения математической задачи применяются численные методы. Как аналитические, так и численные методы решения задач подразделяются на точные и приближенные. К точным относят такие методы, которые позволяют получить решение задачи с любой, заранее заданной точностью. Приближенные методы не предоставляют такой возможности. В этих случаях при построении решения должна быть произведена оценка погрешности. В свою очередь, численные методы решения задач разбиваются на 2 группы. К первой относятся так называемые прямые методы – алгоритмы, позволяющие за конечное, заранее определенное число арифметических действий получить решение задачи. Вторую группу составляют методы последовательных приближений, или так называемые итерационные методы. На рис. 1.2 приведена классификация методов решения вычислительных задач.

 

 

Рис. 1.2. Методы решения вычислительных задач

 

4. Четвертым этапом является разработка программы решения задачи на компьютере, ее тестирование и отладка. Может оказаться так, что рассматриваемая математическая задача исследована, и для ее решения разработаны стандартные программы, которые могут существовать отдельно или входить в пакеты прикладных программ. Тогда остается только выбрать подходящую программу или пакет прикладных программ.

 

5. На заключительном этапе выполняют вычислительные эксперименты на компьютере и проводят анализ результатов. Если результаты не удовлетворяют исследователя, требуется совершенствование алгоритма или метода решения задачи, ее математической модели, а в некоторых случаях — корректировка содержательной постановки.