Элементы теории погрешностей
Определение 1.1. Приближенным значением некоторой величины а называется число ар, которое незначительно отличается от точного значения этой величины.
Пусть а — точное значение некоторой величины, а ар — ее приближенное значение.
Определение 1.2. Абсолютной погрешностью Δ приближенного значения называется модуль разности между точным и приближенным значениями этой величины:
Пример 1.1. Если а = 20.25 и ар = 20, то абсолютная погрешность Δ = 0.25.
Определение 1.3. Относительной погрешностью приближенной величины ар называется отношение абсолютной погрешности приближенной величины к абсолютной величине ее точного значения:
Это равенство можно записать в другой форме:
Пример 1.2. Пусть а = 20.25 и ар = 20, тогда относительная погрешность δ = 0.25/20 = 0.0125. На практике, как правило, точное значение величины неизвестно. Поэтому вместо теоретических понятий абсолютной и относительной погрешностей используют практические понятия предельной абсолютной погрешности и предельной относительной погрешности.
Определение 1.4. Под предельной абсолютной погрешностью приближенного числа понимается всякое число Δа, не меньшее абсолютной погрешности этого числа:
Неравенство (1.5) позволяет для точного значения величины получить оценку
Часто неравенства (1.6) записывают в другой форме
На практике в качестве предельной абсолютной погрешности выбирают наименьшее из чисел Δа, удовлетворяющих неравенству (1.5), однако это не всегда возможно.
Пример 1.3. Оценить предельную абсолютную погрешность приближенного значения ар = 2.72 числа е, если известно, что е = 2.718281828... Решение. Очевидно, что | ар — е |< 0.01. Следовательно, можно положить Δа = 0.01. Также справедливо неравенство | ар — е | = |2.720 – 2.71828... | < 0.002. Получаем другое значение предельной аб солютной погрешности Δа = 0.002. Ясно, что следует выбрать наименьшее из найденных значений предельной погрешности, так как это позволит сузить диапазон (1.5), в котором находится точное значение изучаемой величины.
Определение 1.5. Предельной относительной погрешностью δа данного приближенного числа называется любое число, не меньшее относительной погрешности этого числа: δ <= δа (1.8) Так как справедливо неравенство
то можно считать, что предельные абсолютная и относительная погрешности связаны формулой
Пример 1.4. Пусть длина бруска измерена сантиметровой линейкой и получено приближенное значение ар = = 251 см. Найти предельную относительную погрешность δа. Решение. Так как сантиметровая линейка не содержит делений меньше сантиметра, то предельная абсолютная погрешность Δа = 1 см, а точное значение а длины бруска находится в диапазоне 250 см <= а <= 252 см. Хотя точное значение а неизвестно, можно для относительной погрешности записать неравенство
т. е. считать, что δа = 0,004.
Если предельная абсолютная погрешность Δа значительно меньше точного значения |а|, то предельную относительную погрешность определяют приближенно как отношение абсолютной погрешности к приближенному значению:
Часто в формуле (1.10) вместо знака «≈» используют знак точного равенства «=». Относительную погрешность иногда задают в процентах.
Пример 1.5. Определить предельную относительную и абсолютную погрешности значения х = 125 ± 5%. Решение. Здесь δа = 5% = 0.05 и Δа = 0.05 • 125 = 6.25. В этом примере мы воспользовались формулой (1.10).
|

 (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4)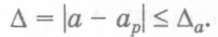 (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7)
 или
или  (1.9)
(1.9)
 (1.10)
(1.10)


