Погрешность произвольной функции
Пусть задана произвольная функция u = f(xl, x2,..., xn), где xl, x2,..., xn — приближенные величины, а Δxl, Δx2, …, Δxn —их известные предельные абсолютные погрешности. Тогда предельная абсолютная погрешность результата — функции u — для малых Δxi. вычисляется по формуле
Как видно из формулы (1.17), для ее применения требуется, чтобы функция f(xl, x2,..., xn) была дифференцируемой по всем переменным.
Пример 1.17. Вычислить функцию u = 2 sin(3x + 4у), если х = π/24±0.002 и y = π/32±0.005. Найти предельные абсолютную и относительную погрешности результата и определить число верных значащих цифр.
|
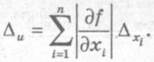(1.17)
