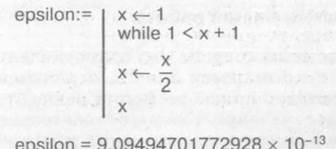Представление чисел в компьютере и погрешность

 

 

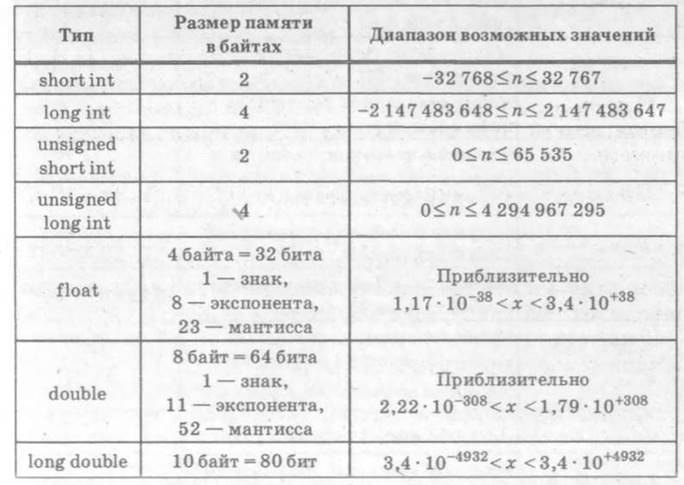
Так как для записи числа в компьютере выделяется ограниченная область памяти, то числовые значения ограничены. Границы значений зависят от типа числа и конкретной среды программирования или математического пакета. В табл. 1.1 представлены диапазоны значений чисел различных типов в языке программирования С.

 

 

Таблица 1.1

 

 

Если при вычислениях для переменной типа float будет получено число с меньшим порядком, чем -38, оно будет заменено нулем, а если порядок числа превысит 38, то произойдет так называемый «аварийный останов» (система прекратит выполнение программы пользователя) и выведено сообщение о переполнении порядка. Для переменной типа float число с меньшим порядком, чем -38, является нулем, а с большим, чем 38, — бесконечностью.

-Для переменной типа double нулем являются значения с меньшим порядком, чем -308, а бесконечностью — значения с порядком большим, чем 308.

В табл. 1.2 приведены константы для чисел с плавающей точкой стандартной библиотеки языка программирования С.

 

Таблица 1.2

 

В программах OpenOffice Calc, Microsoft Excel и Mathcad границы значений числа приблизительно соответствуют типу double языка С. Мантисса может содержать до 15 десятичных цифр. Например, число десятичных знаков числа с плавающей точкой в программе Excel можно найти очень простым способом: записать в ячейку формулу = 1/3 и с помощью команды меню «Формат ячейки» определить формат «числовой с 20 знаками после запятой». Мы увидим, что мантисса числа содержит 15 (значащих) десятичных цифр, остальные цифры равны нулю.

 

Если в программах Excel и Mathcad вычислить значение 1 + 10^-15, то получим 0, а значение выражения 1 + 10^-14 будет равно 1.00000000000001. Это число содержит 15 значащих цифр. Предельной относительной погрешностью представления числа с плавающей точкой в программах Excel и Mathcad можно считать 10^-14.

 

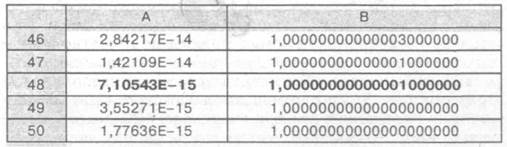
Относительная погрешность представления чисел с плавающей точкой («машинное эпсилон») определяется как наименьшее положительное число ε, при сложении которого с единицей получается отличное от единицы число. Это значение зависит от количества знаков, которые можно записать в мантиссе числа.

Для приблизительной оценки значения относительной погрешности представления можно предложить следующий алгоритм:

1) ε = 1;

2) ε = ε /2;

3) если 1 < 1 + ε, то переходим к п. 2, иначе — переходим к п. 4;

4) выводим значение 2ε.

Вычислим по этому алгоритму в программе Excel значение ε. Для этого вводим в ячейке А1 значение 1, в А2 формулу = А1/2, а в В2 — формулу = 1 + А2. Выделим две ячейки А2:В2 и маркером заполнения протянем вниз до строки 50. В столбце В получим результаты сложения с единицей убывающих чисел из столбца А. В табл. 1.3 приведены последние пять строк вычисленных значений. Очевидно, что за предельную относительную погрешность можно принять значение ε = 7,10543 • 10^-15, или, если округлить, ε = 10^-14, и максимальное число значащих цифр в мантиссе составляет 15.

 

Таблица 1.3

 

Создадим в программе Excel макрос — пользовательскую функцию для определения значения ε.

Выполним команду меню «Сервис — Макрос — Редактор Visual Basic»; в открывшемся окне выберем меню «Insert — Module» и введем описание функции:

Function epsilon ()

eps = 1

2 eps = eps/2

If 1 < 1 + eps Then GoTo 2

epsilon = eps*2

End Function

 

На рис. 1.3 показано окно редактора Visual Basic с введенным текстом программы.

Рис. 1.3

Закроем редактор, перейдем на лист Excel и введем в любой ячейке формулу

= epsilon (), получим значение

ε= 2,22045Е-16 = 0,000 000 000 000 000 222045.

 

Отличие полученного значения ε = 2.22045Е-16 от ε = = 7,10543 • 10^-15 из таблицы 1.2 объясняется особенностями вывода значений в ячейки программы Excel. При выводе числовых значений в ячейки количество значащих цифр равно 15, остальные цифры отбрасываются.

Применим алгоритм вычисления «машинного эпсилон» в системе программирования Mathcad. Однако здесь нас ждут интересные особенности. Введем в Mathcad следующую программу:

 

Мы видим, что число х = 9.09494701772928 10^-13 в неравенстве 1 < х + 1 программа Mathcad принимает за 0, но если мы выполним сложение

1 + 9,09494701772928 • 10^-13, то получим 1,00000000000091. Это означает, что в неравенствах в программе Mathcad относительная погрешность составляет 10^-12. Интересно, что в программе Excel в неравенствах та же относительная погрешность 10^-14, что и в представлении числа с плавающей точкой. Чтобы проверить это, в любой ячейке листа Excel введем неравенство в виде формулы = 1 + 10^-14>1. Получим значение «ИСТИНА». А если ввести формулу = 1 + 10^-15>1, то «ЛОЖЬ». Обращаем здесь внимание на то, что в выражении 10^-15 не обязательно брать в скобки показатель степени -15.

Вычислим «машинное эпсилон» для языка программирования Borland С++. Для этого составим следующую программу:

#include <stdio.h>

int main () {

float eps2, eps = 1, x = 1, y;

do{

eps = eps/2; у = x + eps;

} while (x < y);

eps2 = 2 * eps;

printf ("\neps =%e:", eps2);

return 0;

}

 

В результате выполнения программы получим eps = 1.192093е-07. Это значение совпадает с числом FLT_EPSILON = 1.192093е-07, приведенным в табл. 1.1 (минимально возможное значение переменной типа float, такое, что 1.0 + FLT_EPSILON ≠ 1.0). Если в этой программе мы заменим тип float на тип double, то получим значение eps = 2.220446е-16, которое совпадает с константой DBL_EPSILON.