Рассмотрим раму, изображенную на рис. 13а; степень кинематической неопределимости ее равна трем (n = nу + nл = 2 + 1 = 3); основная система метода перемещений представлена на рис. 13б; погонные жесткости участков
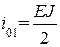 ;
; 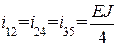 ;
; 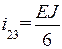 ;
;
удобно выразить через общую для всех участков величину 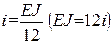 , с учетом которой получим: i 01 = 6 i; i 12 = i 24 = i 35 = 3 i;i 23 = 2 i; (для наглядности эти погонные жесткости участков удобно показать на основной системе метода перемещений (рис. 13б); единичные эпюры изгибающих моментов в основной системе метода перемещений
, с учетом которой получим: i 01 = 6 i; i 12 = i 24 = i 35 = 3 i;i 23 = 2 i; (для наглядности эти погонные жесткости участков удобно показать на основной системе метода перемещений (рис. 13б); единичные эпюры изгибающих моментов в основной системе метода перемещений 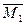 ,
, 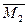 ,
, 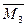 , построены на основе схем деформаций О.С. от перемещений узлов Z 1, Z 2, Z 3, единичной величины (рис. 13в, 13е, 13и) с использованием табличных эпюр (табл.1) и показаны соответственно на рис. 13г, 13ж, 13к; единичные коэффициенты канонических уравнений определяются статическим способом реактивные моменты r 1 K , r 2 K - из вырезания узлов 1 и 2 на эпюрах
, построены на основе схем деформаций О.С. от перемещений узлов Z 1, Z 2, Z 3, единичной величины (рис. 13в, 13е, 13и) с использованием табличных эпюр (табл.1) и показаны соответственно на рис. 13г, 13ж, 13к; единичные коэффициенты канонических уравнений определяются статическим способом реактивные моменты r 1 K , r 2 K - из вырезания узлов 1 и 2 на эпюрах  , а реактивные силы r 3 K - из вырезания верхней части рамы на эпюрах
, а реактивные силы r 3 K - из вырезания верхней части рамы на эпюрах  - см.рис. 13д, 13з, 13л:
- см.рис. 13д, 13з, 13л:
- рис. 13д: 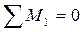 ;
; 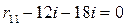 ;
; 
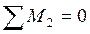 ;
; 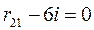 ;
; 
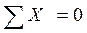 ;
; 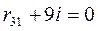 ;
; 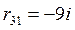
- рис. 13з: 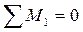 ;
; 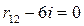 ;
; 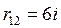
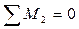 ;
; 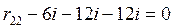 ;
; 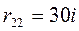
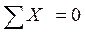 ;
; 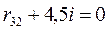 ;
; 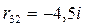
- рис. 13л: 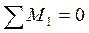 ;
; 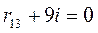 ;
; 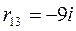
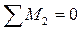 ;
; 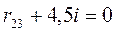 ;
; 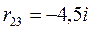
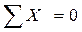 ;
;  ;
; 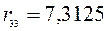
Грузовая эпюра Мр в основной системе метода перемещений представлена на рис. 14а. Грузовые коэффициенты (свободные члены уравнений) определяются по аналогии с единичными (см.рис 14б):
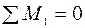 ;
; 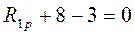 ;
; 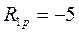
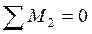 ;
; 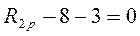 ;
; 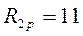
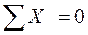 ;
; 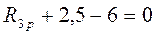 ;
; 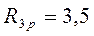
После подстановки найденных значений единичных коэффициентов и свободных членов в систему уравнений (3) получим ее в виде
 30i Z 1 + 6i Z 2 - 9i Z 3 – 5 = 0;
30i Z 1 + 6i Z 2 - 9i Z 3 – 5 = 0;
6i Z 1 + 30i Z 2 – 4.5i Z 3 + 11 = 0;
– 9i Z 1 − 4.5i Z 2 + 7.3125i Z 3 + 3.5 = 0;
решив эту систему уравнений, найдем неизвестные перемещения узлов системы
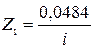 ;
; 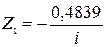 ;
; 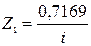 ;
;
после чего окончательная эпюра изгибающих моментов строится по формуле


 М=М 1 Z 1 + М 2 Z 2 + М 3 Z 3 + Мp
М=М 1 Z 1 + М 2 Z 2 + М 3 Z 3 + Мp
и будет иметь вид, представленный на рис. 14в; на рис. 14г показано равновесие узлов 1 и 2 на окончательной эпюре М.
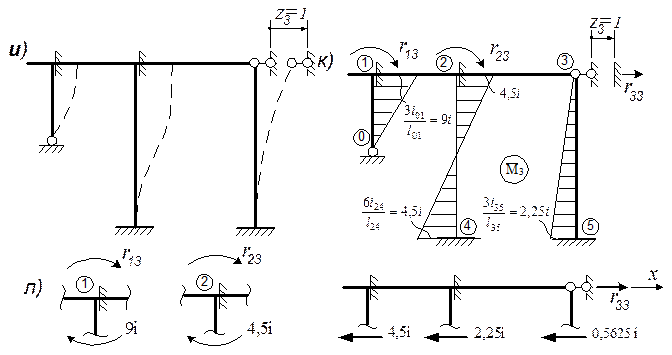
Рис. 13

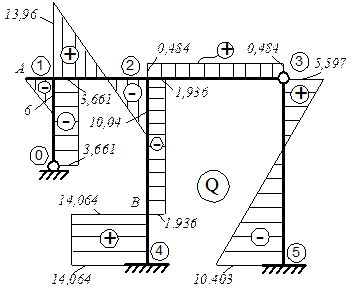 Рис. 14
Рис. 14
Рис. 15 Рис. 16
 Для выполнения деформационной проверки эпюры М выберем для заданной рамы, имеющей четыре лишних связи (Л =4), основную систему метода сил в виде, показанном на рис. 14д; суммарная единичная эпюра
Для выполнения деформационной проверки эпюры М выберем для заданной рамы, имеющей четыре лишних связи (Л =4), основную систему метода сил в виде, показанном на рис. 14д; суммарная единичная эпюра 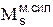 , построенная сразу от всех неизвестных X 1... X 4 единичной величины, показана на
, построенная сразу от всех неизвестных X 1... X 4 единичной величины, показана на
рис. 14e; тогда деформационная проверка запишется в виде:
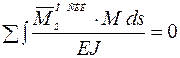 ;
;

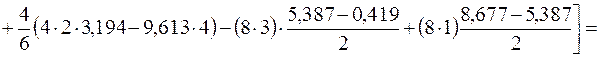
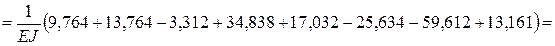
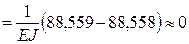 .
.
Эпюру поперечных сил Q построим, вычислив на участках непрерывного изменения эпюры М значения Q по формуле (4):
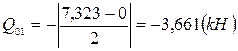 ;
; 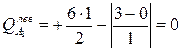 ;
;
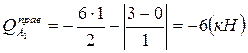 ;
;
 ;
;
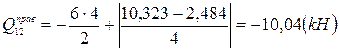 ;
;
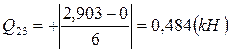 ;
; 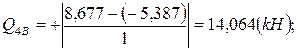
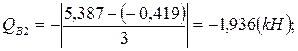
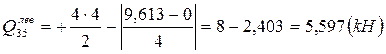
; 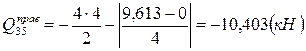 ;
;
Эпюру продольных сил N построим способом вырезания узлов (из эпюры поперечных сил Q):
Узел 1Узел 2Узел 3
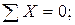 N 12 = -3,661(кн);
N 12 = -3,661(кн);  N 23 = -5,597(кн);
N 23 = -5,597(кн);  5,597 - 5,597=0;
5,597 - 5,597=0;
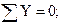 N 10 =-19,96(кн);
N 10 =-19,96(кн); 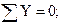 N 24 = -10,524(кн);
N 24 = -10,524(кн); 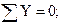 N 35 = +0,484(кн).
N 35 = +0,484(кн).
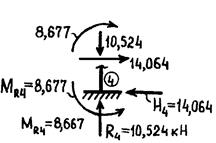
Вырезав опорные узлы, определим опорные реакции:
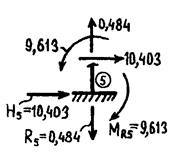 Узел 0Узел 4Узел5
Узел 0Узел 4Узел5
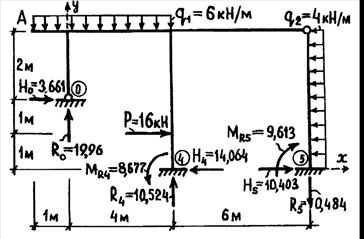
Статическая проверка:
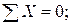
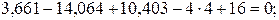
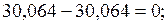
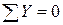 ;
;
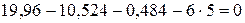
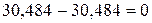 ;
;
Рис. 17
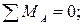 6∙5∙2,5-16∙3+4∙4∙2-3,661∙2+14,064∙4-10,403∙4-19,96∙1-10,524∙5+0,484∙11-8,667+9,613=0; 178,193-178,191
6∙5∙2,5-16∙3+4∙4∙2-3,661∙2+14,064∙4-10,403∙4-19,96∙1-10,524∙5+0,484∙11-8,667+9,613=0; 178,193-178,191 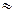 0
0
Все проверки выполняются. Рама рассчитана верно.


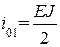 ;
; 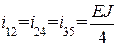 ;
; 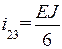 ;
;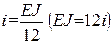 , с учетом которой получим: i 01 = 6 i; i 12 = i 24 = i 35 = 3 i;i 23 = 2 i; (для наглядности эти погонные жесткости участков удобно показать на основной системе метода перемещений (рис. 13б); единичные эпюры изгибающих моментов в основной системе метода перемещений
, с учетом которой получим: i 01 = 6 i; i 12 = i 24 = i 35 = 3 i;i 23 = 2 i; (для наглядности эти погонные жесткости участков удобно показать на основной системе метода перемещений (рис. 13б); единичные эпюры изгибающих моментов в основной системе метода перемещений 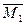 ,
, 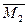 ,
, 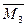 , построены на основе схем деформаций О.С. от перемещений узлов Z 1, Z 2, Z 3, единичной величины (рис. 13в, 13е, 13и) с использованием табличных эпюр (табл.1) и показаны соответственно на рис. 13г, 13ж, 13к; единичные коэффициенты канонических уравнений определяются статическим способом реактивные моменты r 1 K , r 2 K - из вырезания узлов 1 и 2 на эпюрах
, построены на основе схем деформаций О.С. от перемещений узлов Z 1, Z 2, Z 3, единичной величины (рис. 13в, 13е, 13и) с использованием табличных эпюр (табл.1) и показаны соответственно на рис. 13г, 13ж, 13к; единичные коэффициенты канонических уравнений определяются статическим способом реактивные моменты r 1 K , r 2 K - из вырезания узлов 1 и 2 на эпюрах  , а реактивные силы r 3 K - из вырезания верхней части рамы на эпюрах
, а реактивные силы r 3 K - из вырезания верхней части рамы на эпюрах 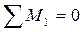 ;
; 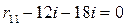 ;
; 
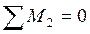 ;
; 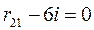 ;
; 
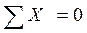 ;
; 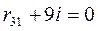 ;
; 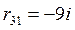
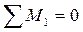 ;
; 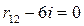 ;
; 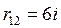
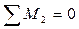 ;
; 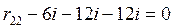 ;
; 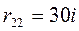
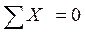 ;
; 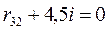 ;
; 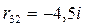
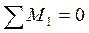 ;
; 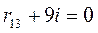 ;
; 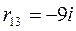
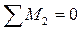 ;
; 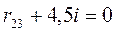 ;
; 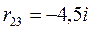
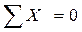 ;
;  ;
; 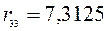
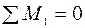 ;
; 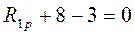 ;
; 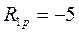
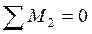 ;
; 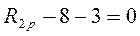 ;
; 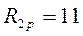
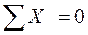 ;
; 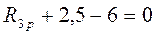 ;
; 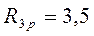
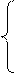 30i Z 1 + 6i Z 2 - 9i Z 3 – 5 = 0;
30i Z 1 + 6i Z 2 - 9i Z 3 – 5 = 0;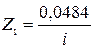 ;
; 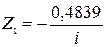 ;
; 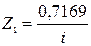 ;
;
 М=М 1 Z 1 + М 2 Z 2 + М 3 Z 3 + Мp
М=М 1 Z 1 + М 2 Z 2 + М 3 Z 3 + Мp
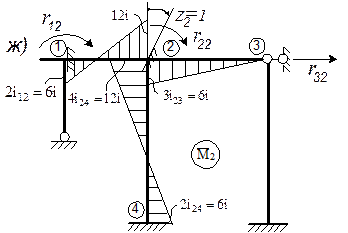
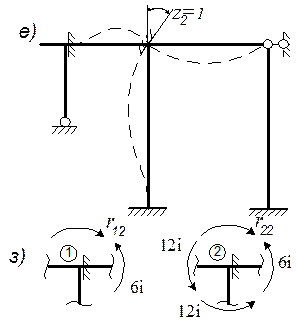
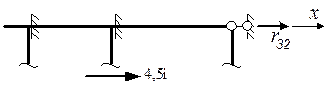




 Рис. 14
Рис. 14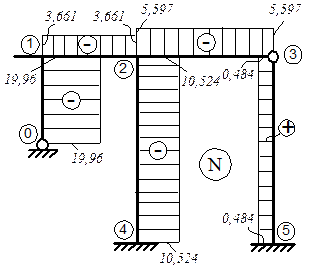
 Для выполнения деформационной проверки эпюры М выберем для заданной рамы, имеющей четыре лишних связи (Л =4), основную систему метода сил в виде, показанном на рис. 14д; суммарная единичная эпюра
Для выполнения деформационной проверки эпюры М выберем для заданной рамы, имеющей четыре лишних связи (Л =4), основную систему метода сил в виде, показанном на рис. 14д; суммарная единичная эпюра 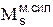 , построенная сразу от всех неизвестных X 1... X 4 единичной величины, показана на
, построенная сразу от всех неизвестных X 1... X 4 единичной величины, показана на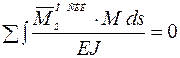 ;
;
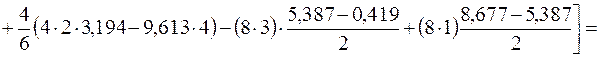
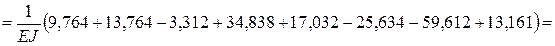
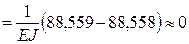 .
.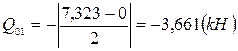 ;
; 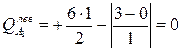 ;
;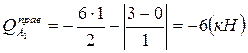 ;
; ;
;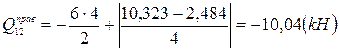 ;
;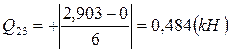 ;
; 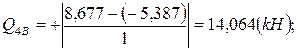
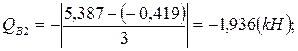
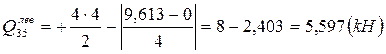
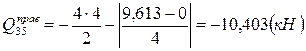 ;
;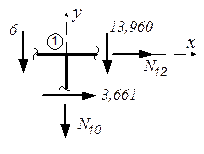
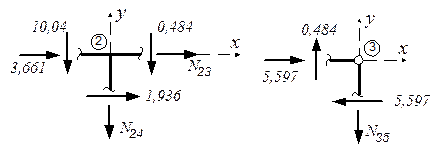
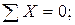 N 12 = -3,661(кн);
N 12 = -3,661(кн);  N 23 = -5,597(кн);
N 23 = -5,597(кн);  N 10 =-19,96(кн);
N 10 =-19,96(кн);  Узел 0Узел 4Узел5
Узел 0Узел 4Узел5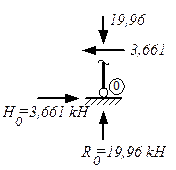

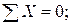
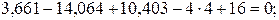
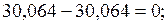
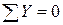 ;
;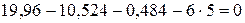
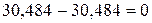 ;
;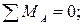 6∙5∙2,5-16∙3+4∙4∙2-3,661∙2+14,064∙4-10,403∙4-19,96∙1-10,524∙5+0,484∙11-8,667+9,613=0; 178,193-178,191
6∙5∙2,5-16∙3+4∙4∙2-3,661∙2+14,064∙4-10,403∙4-19,96∙1-10,524∙5+0,484∙11-8,667+9,613=0; 178,193-178,191 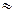 0
0


