УПРОЩЕНИЯ ПРИ РАСЧЕТАХ СИММЕТРИЧНЫХ РАМ
Симметричными называют рамы, которые обладают симметрией относительно некоторой оси (оси симметрии) в конфигурации стержней, в расположении опорных связей и в жесткостях стержней. При расчете симметричных рам методом перемещений, следует применять и использовать все те же подходы, приводящие к упрощениям, что и в методе сил. Основная система метода перемещений при расчете симметричных рам должна удовлетворять всем условиям симметрии, включая разделение всех неизвестных перемещений на симметричные и кососимметричные (обратносимметричные); при этом неизвестные, не удовлетворяющие условиям симметрии, необходимо сгруппировать. В результате система канонических уравнений метода перемещений распадется на две независимые системы, в одну из которых будут входить только симметричные, а во вторую - только кососимметричные неизвестные. Если на раму при этом будет действовать симметричная (кососимметричная) внешняя нагрузка, то все кососимметричные (симметричные) неизвестные, как и в методе сил, обратятся в нуль. Рассмотрим, например, симметричную раму, изображенную на рис. 18а, степень кинематической неопределимости которой равна пяти (n= nу + nл = 2+3 = 5). Основная система для этой рамы в общем случае представлена на рис. 18б, а с учетом группировки неизвестных
на рис. 18в. В результате будем иметь два симметричных (Z 2, Z 4) и три кососимметричных (Z 1, Z 3, Z 5) неизвестных. Общая система уравнений при этом распадается на две независимые системы вида
|
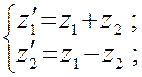
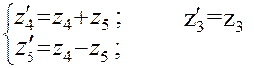
(13) 
(14)
При симметричном нагружении рамы все кососимметричные неизвестные будут равны нулю, т.е. Z 1 = Z 3 = Z 5 = 0, останутся только симметричные неизвестные Z 2, Z 4 и основная система метода перемещений примет вид, показанный на рис. 18 г. Единичные эпюры изгибающих моментов при этом и соответствующие им схемы деформаций показаны на рис. 18д - 18з (построение эпю-
ры М2 на среднем участке нижнего стержня сразу от двух поворотов заделок навстречу друг другу показано на рис. 18и). Значения единичных коэффициентов в этом случае будут:
; 
; 
.
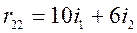При кососимметричной внешней нагрузке на раму на рис. 18а все симметричные неизвестные станут равны нулю (Z 2 = Z 4 = 0), останутся неизвестными перемещения Z 1, Z 3, Z 5 и основная система метода перемещений примет вид, показанный на рис. 19а. Единичные эпюры изгибающих моментов и соответствующие им схемы деформаций показаны на рис. 19в - 19з (при этом построение эпюр М 1 и М 5 на среднем нижнем стержне от одновременного поворота двух заделок по часовой стрелке и их смещения в противоположные стороны представлены на рис. 19б, 19и). Значения единичных коэффициентов здесь будут равны:
; 
; 
;
; 
; 
.
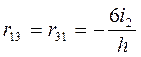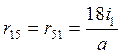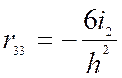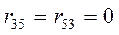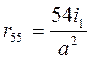