Элементарный вывод формулы Лапласа
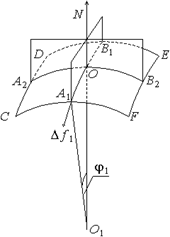
Формулу Лапласа можно получить достаточно просто, если рассмотреть механическое равновесие элемента поверхности раздела. На этой поверхности около произвольной точки O (рис. 29) выделяется малый криволинейный четырехугольник. Пусть ON – внешняя по отношению к первой фазе нормаль к поверхности. Через нее проводятся две взаимно перпендикулярные плоскости, которые пересекаются с поверхностью раздела по некоторым кривым с радиусами кривизны r 1 и r 2 . Малые дуги È A 1 B 1 и È A 2 B 2 – отрезки этих кривых. Элементарная площадка получается, если через концы дуг провести на поверхности кривые, параллельные плоскостям. На рис. 29 это четырехугольник CDEF. С точностью до малых второго порядка È CD = È FE = È A 1 B 1 = ∆ l 1 и È CF = È DE = È A 2 B 2 = ∆ l 2. Площадь четырехугольника равна ∆Σ = ∆ l 1× ∆ l 2. Сила поверхностного натяжения, приложенная к краю CF, в соответствии с формулой (65.2) равна ∆ f 1 = σ∆ l 2. Ее проекция на OO 1 будет
∆ f 1 sin φ1» ∆ f 1 φ1 = ∆ f 1 ∆ l 1 / (2 r 1) =
= σ / (2 r 1) × ∆Σ.
Такое же значение имеет проекция силы натяжения, действующей по краю DE. Поэтому результат удвоится (ради простоты считается, что дуги È A 1 B 1 и È A 2 B 2 делятся точкой O пополам). Аналогичным образом находится проекция сил поверхностного натяжения, приложенных по CD и FE. В результате сила давления, действующая на первую фазу со стороны элемента изогнутой поверхности, равна σ (1/ r 1 + 1/ r 2) × ∆Σ и для давления получается формула Лапласа.
|