Закон действующих масс
Пусть в однородной термодинамической системе протекают химические реакции. Из опыта известно, что всякая химическая реакция может идти как в прямом, так и обратном направлениях. При отсутствии равновесия в системе преобладает либо та, либо другая из них. В равновесном состоянии скорости обеих реакций одинаковы и масса вещества каждого сорта не меняется с течением времени. Уравнение химической рекции записывается в виде
Σν i A i = 0, (69.1)
где A i – химические символы веществ, участвующих в реакции, ν i – стехиометрические коэффициенты (они указывают число молекул веществ, возникающих при ν i > 0 и исчезающих, когда ν i < 0, в одном акте реакции). Например, для реакции
2H2+ O2 = 2H2O, или 2H2O – 2H2 – O2 = 0,
символы A i и ν i имеют значения: A1 = H2O, ν1 = 2; A2 = H2, ν2 = – 2; A3 = O2, ν3 = – 1. Если система помещена в термостат с постоянными температурой и давлением, то равновесие наступает, когда достигается минимум термодинамического потенциала Гиббса (для него естественные переменные T и p):
δ G =
Здесь δ Ni – возможные изменения числа молекул реагирующих веществ. Они пропорциональны коэффициентам уравнения реакции:
δ Ni = δλ × ν i.
При исключении δ Ni из равенства (69.2) получается условие химического равновесия
(μ i – химический потенциал i -го компонента смеси). Если в системе протекает не одна, а несколько химических реакций, то равновесие определяется совокупностью уравнений вида (69.3). Для конкретных приложений необходимо знать выражения для химических потенциалов. В случае идеальных газов они легко могут быть найдены с помощью соотношений
G = U – TS + pV,
U =
piV = NikT, i = 1, 2, …; p =
в которых Ni – число молекул i -го сорта; pi – парциальное давление; ε i – внутренняя энергия, приходящаяся на одну молекулу соответствующего сорта при T = 0 (так называемая нулевая энергия); теплоемкости cV и cp рассчитываются на одну частицу. Отсюда находится
μ i =
При использовании соотношения Майера cpi – cVi = k выражение для химического потенциала принимает вид
μ i = cpiT + ε i – cpiT ln T + kT ln pi – S 0 i T.
Если ввести теперь концентрацию i -го компонента
ci = pi / p
и обозначить через χ i выражение
cpiT + ε i – cpiT ln T – S 0 i T = χ i (T),
то
μ i = kT ln (ci × p) + χ i (T). В результате условие равновесия (69.3) приводится к виду
откуда
и
Эта формула выражает закон действующих масс. Величина
Kc (p, T) =
называется константой химического равновесия. Левая часть формулы (69.4) представляет собой фактически дробь, в числителе которой стоят концентрации продуктов реакции, а в знаменателе – концентрации веществ, вступающих в реакцию. Чем больше константа химического равновесия Kc, тем равновесие в большей степени смещено в сторону конечных продуктов реакции. Если сумма Σν i > 0, то при увеличении давления уменьшаются константа равновесия и выход продуктов реакции. При Σν i < 0, наоборот, константа равновесия и выход продуктов реакции возрастают при увеличении давления. Когда Σν i = 0, выход конечных продуктов не зависит от давления. Для того чтобы выяснить характер зависимости константы равновесия от температуры, находится производная
(∂ln Kc / ∂ T) p = (штрих означает дифференцирование по температуре). С учетом выражения для χ i эта производная равна
(∂ln Kc / ∂ T) p = 1 / (kT 2) ×
В скобках под знаком суммы стоит энтальпия, приходящаяся на одну молекулу i -го компонента, т. е. ε i + cpiT = hi. (69.5)
Сумма же представляет изменение энтальпии в одном акте реакции
Δ h =
или количество теплоты, поглощаемое при реакции, если она протекает изобарически. В термохимии вводится величина, противоположная по знаку Δ h, – тепловой эффект реакции. Это количество теплоты, выделяющееся в реакции. Если в результате реакции получается какое-либо определенное химическое соединение, то тепловой эффект называют также теплотой образования этого соединения. Тепловой эффект реакции зависит лишь от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от промежуточных стадий реакции. Это положение было установлено эмпирически русским академиком Гессом в 1840 г. и называется законом Гесса. Поскольку реакция (69.1) идет при постоянном давлении, то ее тепловой эффект равен
q = – Δ h = –
и зависимость константы равновесия от температуры определяется соотношением
(∂ln Kc / ∂ T) p = – q / (kT 2). (69.7)
В случае эндотермической реакции q < 0 и, следовательно, с ростом температуры константа равновесия и выход продуктов реакции возрастают. При экзотермической реакции (q > 0) повышение температуры ведет к уменьшению константы равновесия и выхода продуктов реакции.
|

 =
= 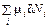 = 0, (69.2)
= 0, (69.2)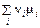 = 0 (69.3)
= 0 (69.3) , S =
, S =  ,
, (закон Дальтона),
(закон Дальтона),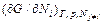 = cViT + ε i – T (cpi ln T – k · ln pi + S 0 i ) + kT.
= cViT + ε i – T (cpi ln T – k · ln pi + S 0 i ) + kT.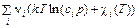 = 0,
= 0, = –
= – 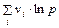 –
– 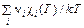
 = Kc (p, T). (69.4)
= Kc (p, T). (69.4)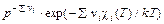
 –
–  = 1/ kT 2×
= 1/ kT 2× 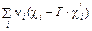
 .
.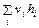 ,
,


