Lt; Рb,e < 1.
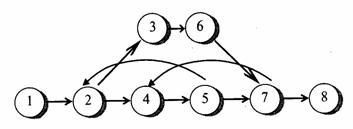
5. Каждой детерминированной дуге (i, j) соответствует вектор, характеризующий параметры работы — время ее выполнения, стоимость, ресурсы. Стохастический граф G(I, U) с возможным возвратом в отдельных фрагментах проекта на доработку строится в несколько этапов. Сначала строится сетевой график G(Iд, Uд). При этом считается, что такой сетевой график соответствует детерминированной части разработки и отражает процесс создания изделия в идеальном случае. На втором этапе выделяются события сетевого графика G(Iд, Uд), после которых может возникнуть необходимость возврата на предыдущие этапы разработки. Далее, возможные исходы всех событий, порождающих возврат, отображаются дугами возврата. Из любого события может исходить несколько дуг возврата, если предвидится несколько причин возврата на доработку. Вероятности возврата этих дуг могут быть связаны между собой различными условиями, учитываемыми при моделировании событий возврата и исходящих из него дуг. Формально сетевой график G(Iд, Uд) дополняется дугами возврата (b, е) и преобразуется в стохастический граф G(I, U), при этом возможно изменение топологии исходного сетевого графика. Фрагмент графа с возвратом приведен на рис. 10.3. После построения стохастического графа дается количественная оценка его параметров. Отличительной особенностью рассматриваемой модели является обязательное выполнение всех входящих в граф G(Iд, Uд) работ, причем некоторые могут выполняться из-за возврата неоднократно. Для изменения продолжительности повторяемых работ вводится коэффициент αij, который определяется отношением продолжительности tij* работы (i, j) при ее повторном выполнении к первоначальной продолжительности этой работы tij, то есть αij, = tij* / tij. . Как правило, 0 < αij < 1. Дуга возврата описывается дополнительным параметром Рb,e — вероятностью возникновения данного вида возврата. Величина вероятности может существенно влиять на параметры графа. Таким образом, стохастический характер и цикличность процесса выполнения комплекса работ по освоению новой продукции обусловливают адекватность его отображения с помощью имитационной модели, основанной на графе с возвратом. Для графа с возвратом вводится ряд специфических временных параметров, часть из которых представляет собой развитие соответствующих характеристик сетевого планирования. Раннее время наступления события I — это время, необходимое для попадания из начального события в событие i в последний раз при движении по наименее благоприятному пути с учетом наступления возврата. Раннее время наступления конечного события графа совпадает с критическим временем реализации всего проекта. Позднее время наступления события i — это время наступления события i в последний раз, превышение которого приведет к увеличению критического времени.
Рис. 10.3. Граф с возвратом Эти параметры не полностью описывают стохастический граф с возвратом, а характеризуют его однократную реализацию. Поэтому дополнительно вводятся статистические параметры графа, описывающие его в среднем, такие, как математическое ожидание и дисперсия времени реализации проекта, вероятность совершения события не позже заданного срока, гистограммы и выборочные функции распределения вероятностей времени совершения конечного и других наиболее важных событий, а также стоимость выполнения комплекса операций. Алгоритм анализа графа с возвратом основан на использовании метода статистических испытаний и известного алгоритма Форда для сетевых графиков. Процедура Форда используется для расчета временных параметров отдельных фрагментов графа с учетом их топологии и задаваемых характеристик, а методами Монте-Карло имитируется реализация соответствующих дуг возврата. Таким образом, центральной процедурой алгоритма является моделирование событий контроля и согласования методом статистических испытаний. Исходы этих событий описываются вероятностями повторного исполнения определенных фрагментов проекта. В результате расчетов модели на ЭВМ определяется ожидаемая (прогнозная) оценка длительности и стоимости разработки новой продукции. Для исследования возможностей сокращения длительности и стоимости процесса могут быть проведены вариантные расчеты по модели, направленные на выявление резервов сокращения длительности работ и вероятности возврата и ранжирование по важности организационно-экономических мероприятий, направленных на интенсификацию инновационного процесса. Следует отметить самостоятельную методическую важность первого этапа — построения сетевой модели процесса разработки и реализации стратегических решений, так как в ходе выполнения данного этапа проводится структуризация работ и установление необходимых взаимосвязей между ними. Тем самым обеспечивается комплексное представление работ по реализации стратегических решений и необходимая интеграция деятельности подразделений, участвующих в его реализации. Важно только, чтобы в этой работе участвовали все подразделения, от которых зависит успех реализации анализируемого стратегического решения. В первую очередь это касается отдела маркетинга, который должен включиться в проект на начальной стадии. В заключение отметим, что описанный модельный аппарат может быть использован не только для анализа продуктовых инноваций, но для любых стратегических программ по внедрению нововведений: новых технологий, новых методов планирования и управления, для которых характерными являются ситуации типа «контроль—доработка». Вопросы и задания 1. В чем суть программно-целевого планирования? 2. Обсудите проблемы, связанные с построением «дерева целей» предприятия. 3. Как, по вашему мнению, можно увязать целевую программу и план предприятия? 4. Обсудите сильные и слабые стороны использования стохастических сетевых моделей в стратегическом менеджменте. Рекомендуемая литература 1. Джонсон Р., Каст Ф., Розенцвейг Д. Системы и руководство — М.: Прогресс, 1971. 2. Комплексная программа развития предприятий непрерывного производства/Коллектив авторов под рук. Н. Б. Мироносецкого и Б В Прилепского. — Новосибирск, 1993. 3. Лоно Т. Стратегия и структура японских предприятий. — М • Прогресс, 1987. 4. Мироносецкий Н. Б., Кирина Л. В., Кузнецова С. А., Маркова В Д и др. Модели научно-технического прогресса на предприятии. - Новосибирск-Наука, 1988. 5. Управление научно-техническими программами/Под ред Д Н Бобрышева. - М.: Экономика, 1986. ПРИЛОЖЕНИЕ 1
|