Следствия теоремы о базисном миноре. Линейная зависимость системы столбцов матрицы, ранг
которой меньше числа столбцов. Теорема о ранге матрицы.) Если ранг матрицы меньше числа ее строк (столбцов), то ее строки (столбцы) линейно зависимы. Если
№11 (Методы элементарных преобразований и окаймляющих миноров вычисления ранга матрицы.)
Элементарными преобразованиями матрицы называются следующие:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от нуля;
3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число. Метод окаймляющих миноров. Пусть в матрице найден минор k -го порядка M, отличный от нуля. Рассмотрим лишь те миноры (k +1)− го порядка, которые содержат в себе (окаймляют) минор M: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор (k +1)−го порядка, и вся процедура повторяется.
Метод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования матрицу можно привести к такому виду, когда все ее элементы кроме a11, a22,..., arr (r≤min(m,n)), равны нулю. Следовательно, ранг матрицы равен r.
№12 (Совместность СЛАУ. Теорема Кронекера-Капелли.)
СЛАУ называется совместной, или разрешимой, если она имеет, по крайней мере, одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений. Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. №13 (Однородные СЛАУ. Свойства решений. Условие нетривиальной совместности. Ядро матрицы.)
|

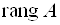 равен числу ее строк (столбцов), то строки (столбцы) линейно независимы.
равен числу ее строк (столбцов), то строки (столбцы) линейно независимы.



