Условие нетривиальной совместности. Ядро матрицы
Для того, чтобы однородная система имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных. Ядро матрицы А – это множество векторов х таких, произведение матрицы А на которые равно нулевому вектору. Поиск ядра матрицы А эквивалентен решению системы линейных однородных уравнений. Ядром матрицы A являются все решения уравнения AW=0.
№14 (Фундаментальная система решений однородной СЛАУ (ФСР). Теорема о существовании ФСР) Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов. Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР. Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.
№15 (Теорема об общем решении однородной СЛАУ) Общим решением линейной системы называется выражение, позволяющее вычислить все (любое) решения системы.
№16 (Алгоритм решения однородных систем линейных алгебраических уравнений.)
1) Выражаем одно из неизвестных (пусть первое
2) Подставляем это неизвестное в другое уравнение из системы (пусть во второе)
Теперь во второй строке мы таким образом избавились от переменного значит, в этом уравнении осталось
3) Выражаем любое из этих
Вот такое страшное выражение получится, если честно раскрыть все скобки и выразить
4) Подставляем выражение для
5) Так проделываем со всеми строками, пока не дойдём до последней. В последней строке у нас останется одно неизвестное (в нашем случае
6) Найдя значение неизвестного
7) Подставляем значения Следовательно, находим
Проделав это со всеми
№17 (Теорема об общем решении неоднородных СЛАУ)
№18 (Алгоритм решения неоднородных СЛАУ.) №19 (Исследование систем линейных алгебраических уравнений с помощью метода Гаусса.) Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Метод Гаусса с выбором главного элемента по всей матрице (схема полного выбора).
На 1-м шаге метода среди элементов aij определяют максимальный по модулю элемент. Первое уравнение системы и уравнение с номером i1 меняют местами. Далее стандартным образом производят исключение неизвестного xi1 из всех уравнений, кроме первого.
Будем называть его главным элементом 1-го шага.
Найдем величины qi1 = ai1/a11 (i = 2, 3, …, n), называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q21, q31, …, qn1. Это позволит обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1
a22x2 + a23x3 + … + a2nxn = b2
a33x3 + … + a3nxn = b3
………………………………………
annxn = bn
Матрица A является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение xn в предпоследнее уравнение, получим xn–1. Осуществляя обратную подстановку, далее последовательно находим xn–1, xn–2, …, x1.
№20 (Векторная алгебра. Основные определения. Линейные операции над векторами.)
Опр.1 Вектором называется направленный отрезок, имеющий определенную длину. Опр.2 Длиной вектора АВ называется его модуль и обозначается символом АВ. Модуль вектора а обозначается а. Опр.3 Вектор называется единичным, если его длина равна единице, т.е. а 1. Вектор называется нуль - вектором, если его длина равна нулю, т.е. а 0, обозначается 0 (нуль – вектор не имеет направления, его начало и конец совпадают). Опр.4 Два вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых, в противном случае вектора – неколлинеарные. Три вектора называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости, в противном случае вектора – некомпланарными. Опр.5 Два вектора называются равными, если они коллинеарные, одинаково направленные и имеют одинаковую длину Опр.6 Вектор, образованный из данного вектора параллельным переносом, называется свободным. Линейные операции над векторами. Линейными операциями называются операции сложения векторов, вычитания векторов и умножение вектора на число. Опр.7 Суммой нескольких векторов называется вектор, по величине и направлению равный замыкающей ломаной линии, построенной на свободных векторах, соответствующих данным векторам, его начало совпадает с налом первого, а конец с концом последнего
№21 Набор векторов Система из Свойства линейно зависимых и линейно независимых векторов 1. Если в систему векторов входит нулевой вектор, то она линейно зависима. 2. Если в системе векторов имеется два равных вектора, то она линейно зависима. 3. Если в системе векторов имеется два пропорциональных вектора 4. Система из 5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему. 6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима. 7. Если система векторов №22 Пусть на плоскости задан ненулевой вектор
При этом Если на плоскости заданы два ненулевых, неколлинеарных вектора При этом совокупность
Если в пространстве заданы три ненулевых, некомпланарных (а, следовательно, линейно независимых) вектора
№24 Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из двух векторов нулевой, то угол между ними не определён, а скалярное произведение считается равным нулю. Скалярное произведение векторов
Где
Скалярное произведение вектора самого на себя
|


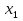 ) из какого-нибудь
) из какого-нибудь 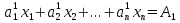 )
) 

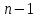 неизвестных:
неизвестных: 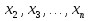
 ) из второго уравнения системы и подставляем его в другую строку, отличную от тех, из которых мы уже выражали какие-то неизвестные (допустим, подставим в третью строку):
) из второго уравнения системы и подставляем его в другую строку, отличную от тех, из которых мы уже выражали какие-то неизвестные (допустим, подставим в третью строку):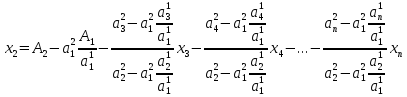

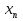 ) Значит, из последней строки мы можем найти численное значение
) Значит, из последней строки мы можем найти численное значение  и
и 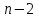 уравнение, в котором 3 неизвестных —
уравнение, в котором 3 неизвестных — 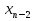 ,
,  уравнениями, мы найдём все
уравнениями, мы найдём все  называется системой векторов. Система из
называется системой векторов. Система из  векторов
векторов 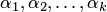 , не все равные нулю одновременно, что
, не все равные нулю одновременно, что 
 , т.е. когда линейная комбинация в левой части равенства тривиальная.
, т.е. когда линейная комбинация в левой части равенства тривиальная.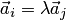 , то она линейно зависима.
, то она линейно зависима. векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных. оказывается линейно зависимой, то вектор
оказывается линейно зависимой, то вектор  , тогда для любого вектора
, тогда для любого вектора  , лежащего на этой же прямой, существует единственное вещественное число
, лежащего на этой же прямой, существует единственное вещественное число 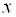 , такое, что
, такое, что
 и
и  , то для любого вектора
, то для любого вектора  и
и 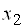 таких, что
таких, что 
 – координатами
– координатами  , то для любого вектора
, то для любого вектора  таких, что
таких, что 
 обозначается
обозначается
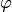 — величина угла между векторами
— величина угла между векторами 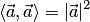 называется скалярным квадратом.
называется скалярным квадратом.


