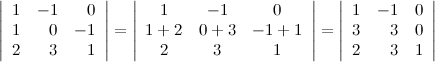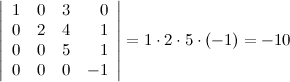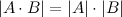Действия над матрицами
1) Сумма матриц. Суммой двух матриц Обозначается 2) Разность матриц. Разностью 3) Умножение матрицы на число. Произведением матрицы 4) Произведение матриц. Пусть даны две матрицы
5) Транспонирование матрицы. Матрица №2 (Перестановки и подстановки. Понятия инверсии и четности.)
№3 (Определитель. Определение, свойства.)
Квадратной матрице
соответствие число
Свойства определителей:
1) При транспонировании квадратной матрицы её определитель не меняется:
2) Общий множитель в строке можно выносить за знак определителя.
3)
4) Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.
5) Если две строки определителя поменять местами, то определитель поменяет знак.
6) Определитель с двумя равными строками равен нулю
7) Определитель с двумя пропорциональными строками равен нулю.
8) Определитель, содержащий нулевую строку, равен нулю.
9) Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Пусть задан определитель третьего порядка
10) Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
11) Определитель произведения матриц равен произведению определителей:
|

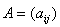 и
и 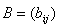 одинакового размера называется матрица
одинакового размера называется матрица 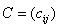 того же размера, элементы которой находятся по формуле:
того же размера, элементы которой находятся по формуле: 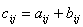
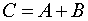
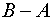 матриц
матриц 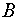 и
и 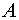 одинакового размера называется такая матрица
одинакового размера называется такая матрица 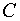 , что
, что 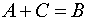
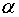 называется матрица
называется матрица 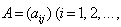
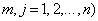 и
и 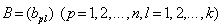 размерностей
размерностей 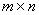 и
и 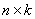 соответственно, причем число столбцов
соответственно, причем число столбцов 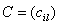 , элементы которой находятся по формуле:
, элементы которой находятся по формуле: 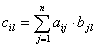 . Обозначается
. Обозначается 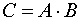
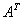 , полученная из данной матрицы A заменой каждой строки на столбец с тем же номером, называется матрицей, транспонированной к данной матрице А. Иными словами, при транспонировании матрицы ее строки и столбцы меняются местами.
, полученная из данной матрицы A заменой каждой строки на столбец с тем же номером, называется матрицей, транспонированной к данной матрице А. Иными словами, при транспонировании матрицы ее строки и столбцы меняются местами.
 n – го порядка ставиться в
n – го порядка ставиться в , называемое определителем матрицы или детерминантом.
, называемое определителем матрицы или детерминантом.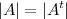
 То есть, если квадратная матрица
То есть, если квадратная матрица 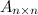 n – го порядка умножается на некоторое ненулевое число
n – го порядка умножается на некоторое ненулевое число 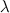 то определитель полученной матрицы равен произведению определителя исходной матрицы
то определитель полученной матрицы равен произведению определителя исходной матрицы 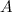 на число
на число 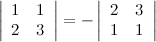
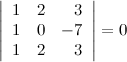
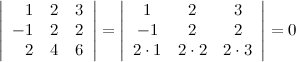
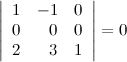
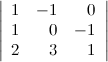 Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:
Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться: