Показатели измерения парной линейной корреляции
Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла или коэффициент контингенции К. Пирсона. Расчетная таблица в этом случае состоит из четырех ячеек (таблица «четырех полей»), статистическое сказуемое которой схематически может быть представлено в следующем виде:
где: а, b, с, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков; п - общая сумма частот. Коэффициент ассоциации исчисляется по формуле:
Коэффициент контингенции:
Коэффициент контингенции по значению всегда меньше коэффициента ассоциации. Связь считается достаточно значимой и подтвержденной, если | Ка | > 0,5 или | Кк | >0,3 Для оценки тесноты связи между альтернативными признаками, принимающими любое число вариантов значений, применяется коэффициент взаимной сопряженности К. Пирсона и А.А.Чупрова. Первичная статистическая информация для исследования этой связи располагается в форме таблицы:
где mij - частоты взаимного сочетания двух атрибутивных признаков; n - число пар наблюдений. Коэффициент взаимной сопряженности Пирсона определяется по формуле:
Коэффициент взаимной сопряженности Чупрова:
где f2 - показатель взаимной сопряженности; К1, К2 – число строк и граф в таблице.
или в общем виде
Коэффициент взаимной сопряженности изменяется от 0 до 1. Биссериальный коэффициент корреляции – дает возможность оценить связь между качественным альтернативным и количественным варьирующим признаками.
p – доля первой группы; q - доля второй группы; z – табличные значения Z -распределения в зависимости от p.
В тех случаях, когда одна переменная измеряется в дихотомической шкале (переменная X), а другая в ранговой шкале (переменная Y), используется рангово-бисериальный коэффициент корреляции. Особо необходимо подчеркнуть, то что этот коэффициент изменяется в диапазоне от -1 до +1, его знак для интерпретации результатов не имеет значения. Это еще одно исключение из общего правила. Расчет этого коэффициента производится по формуле:
N - общее количество элементов в переменной X Для применения рангово-бисериального коэффициента корреляции необходимо соблюдать следующие условия: 1. Сравниваемые переменные должны быть измерены в разных шкалах одна X - в дихотомической шкале, другая Y - в ранговой шкале 2. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым 3. Для оценки уровня достоверности рангово-бисериального коэффициента корреляции следует пользоваться формулой (приведенной выше) и таблицей критических значений для t -критерия Стьюдента при k = n – 2. К показателям степени тесноты связи относят коэффициент корреляции знаков, который был предложен немецким ученым Г.Фехнером (1801-1887). Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Для его расчета вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков. Если ввести обозначения: па - число совпадений знаков отклонений индивидуальных величин от средней, пв - число несовпадений знаков отклонений, то коэффициент Фехнера можно записать таким образом:
Коэффициент Фехнера может принимать различные значения в пределах от -1 до +1. Если знаки всех отклонений совпадут, то пв = 0 и тогда показатель будет равен 1, что свидетельствует о возможном наличии прямой связи. Если же знаки всех отклонений будут разными, тогда п а = 0 и коэффициент Фехнера будет равен -1, что дает основание предположить наличие обратной связи. Как видно из приведенной формулы для расчета коэффициента Фехнера, величина этого показателя не зависит от величины отклонений факторного и результативного признака от соответствующей средней величины. Поэтому нельзя говорить о степени тесноты корреляционной связи, а тем более об оценке ее существенности на основании только коэффициента Фехнера. При малом объеме исходной информации коэффициент Фехнера практически решает ту же задачу, которая ставится при построении групповых и корреляционных таблиц, т.е. отвечает на вопрос о наличии и направлении корреляционной связи между признаками. Более совершенным показателем, используемым для измерения тесноты связи как качественных, так и количественных факторов, при условии, что их значении можно проранжировать, является ранговый коэффициент корреляции Спирмена (также называемый коэффициент корреляции рангов Спирмена по имени английского психолога разработавшего данный коэффициент Ч.Спирмена (1863-1945)) который имеет вид:
RiX, RiY - ранги по результативному и факторному признаку; n – объем изучаемой совокупности. Ранжирование – процедура упорядочения объектов изучения, которая выполняется на основе предпочтения. Ранг – это порядковый номер единицы совокупности в ранжированном ряду. Коэффициент корреляции Спирмена может принимать значения от 0 до ± 1. Преимущество коэффициента корреляции рангов состоит в том, что на его основе оценивается коррелированность качественных признаков, не имеющих точного количественного измерения. Коэффициент линейной корреляции был предложен английским статистиком К.Пирсоном. Его интерпретация такова: отклонение признака-фактора от его среднего значения на величину своего среднего квадратического отклонения в среднем по совокупности приводит к отклонению признака-результата от своего значения на r его среднего квадратического отклонения. Коэффициент корреляции является отвлеченным показателем, характеризующим тесноту связи между переменными, если эта связь линейная. Одной из формул расчета показателя является следующая:
Коэффициент корреляции обладает следующими свойствами: Принимает значения на отрезке [-1;1] 0 – связь между x и y отсутствует; (0-0,3] - связь присутствует но она незначительна; (0,3-0,5] - умеренная связь; (0,5-0,7] - средняя связь; (0,7-0,99] - тесная связь; 1 - связь между x и y функциональная. Следующий коэффициент – коэффициент детерминации, равный квадрату коэффициента корреляции
|

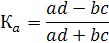


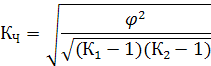

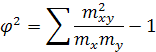
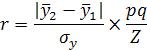
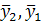 – средняя в группах;
– средняя в группах; – среднее квадратическое отклонение фактических значений признака от среднего уровня;
– среднее квадратическое отклонение фактических значений признака от среднего уровня;
 - средний ранг по тем элементам переменной Y, которым соответствует код (признак) 1 в переменной X;
- средний ранг по тем элементам переменной Y, которым соответствует код (признак) 1 в переменной X;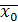 - средний ранг по тем элементам переменной Y, которым соответствует код (признак) 0 в переменной X;
- средний ранг по тем элементам переменной Y, которым соответствует код (признак) 0 в переменной X;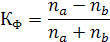


 , выраженный в процентах и показывающий, какой процент вариации результата признака объясняется вариацией факторного признака.
, выраженный в процентах и показывающий, какой процент вариации результата признака объясняется вариацией факторного признака.


