IV. Сприймання і усвідомлення поняття arccos a і властивостей функціїу = arccos x. Функція у = cos x спадає на відрізку [0; π] і приймає всі значення від -1 до 1, тому рівняння cos x = а, | а | < 1 на проміжку [0; π] має єдиний корінь, який називається арккосинусом числа а і позначається arccos a.
Арккосинусом числа а називається таке число з проміжку[0; π], косинус якого дорівнює а. Приклад 1. Знайдіть arccos arccos Приклад 2. Знайдіть arccos arccos Виконання вправ 1. Обчисліть: a) arccos r) arccos (-1); д) arccos1; є) arccos Відповідь: a) 2. Які з поданих виразів мають смисл і чому: a) arccos г) arccos Відповідь: б); д); е). 3. Знайдіть: a) arccos Відповідь: a)
Розглянемо властивості функції у = arccos х. 1. D (y) = [-1; 1]. 2. Е(y)=[0;π]. 3. Графік не симетричний ні відносно початку координат, ні відносно осі OY. arccos (- х) = π - arccos х. 4. Функція спадна. Якщо х 1 > х 2 то arccos х 1 <; arccos х 2. 5. у = 0, якщо х = 1. 6. у mах = y (-1) = π, y mіn = y (1) = 0.
|
.
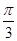, бо cos 
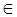[0;π].
.
, бо cos 
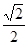і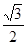 
; б) arccos 
.
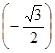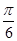; б) 
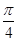; в)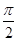 
; г) π; д) 0; є) 
.
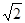; б) arccos 
; в) arccos 
;
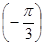; д) arccos 
; є) arccos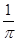 
?
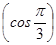; б) arccos 
; в) cos (arccos (-1)).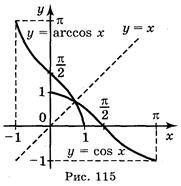
Аналогічно можна говорити про функцію у = arccos x. Графік функції у = arccos x одержимо із графіка функції у = cos x, x 
