VI. Сприймання і усвідомлення поняття arcctg a і властивостей функції
у = arcctg х. Функція у = ctg х на інтервалі (0; π ) спадає і приймає всі значення із R, тому для будь-якого числа а в інтервалі (0; π) існує єдиний корінь рівняння ctg х = а. Це число називають арккотангенсом числа а і позначають arcctg a.
Арккотангенсом числа а називається таке число із інтервалу (0; π ), котангенс якого дорівнює а. Приклад 1. arcctg Приклад 2. arcctg Виконання вправ 1. Обчисліть: a) arcctg 1; б) arcctg Відповідь: а)
Укажемо властивості функції у = arcctg х: 1. D(y)=R. 2. E(y) = (0; π ). 3. Графік не симетричний ні відносно початку координат, ні відносно осі OY. arcctg (-х) = π - arcctg х. 4. Функція спадна. Якщо х 1< х 2 то arcctg х 1 > arcctg х 2. 5. х = 0, якщо у = 6. у > О для всіх х Значення обернених тригонометричних функцій можна обчислювати за допомогою таблиць або мікрокалькулятора.
|

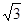 =
= 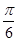 , бо ctg
, бо ctg 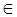 (0; π).
(0; π). =
=  , бо ctg
, бо ctg 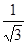 ; в) arcctg 0; г) arcctg (-1); д) arcctg
; в) arcctg 0; г) arcctg (-1); д) arcctg  .
.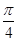 ; б)
; б) 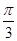 ; в)
; в) 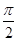 ; г)
; г)  ; д)
; д)  .
. Графік функції у = arcctg x можна одержати із графіка функції у = ctg x у результаті перетворення симетрії відносно прямої у = х (рис. 121).
Графік функції у = arcctg x можна одержати із графіка функції у = ctg x у результаті перетворення симетрії відносно прямої у = х (рис. 121).


