Доходность портфеля в условиях нечетких случайных данных.Пусть Введем также нечеткие случайные величины Тогда, на основании результатов первой главы, доходность портфеля может быть представлена нечеткой случайной величиной:
Ее математическое ожидание Понятно, что при фиксированном
Ее распределение может быть определено по формулам, полученным в первой главе диссертации. Ожидаемая доходность отдельного финансового актива есть Таким образом, мы видим, что ожидаемая доходность портфеля есть нечеткая величина. Поэтому нам необходимо провести обобщение моделей Марковица, дающее возможность производить «глубинную» обработку толерантных временных рядов для получения временных рядов, позволяющих оценить параметры распределений.
|
-доля капитала, выделяемая на покупку ценных бумаг 
-го вида, такая что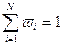 
, 
, 
.
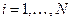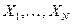, представляющие доходности финансовых активов: 
.
.
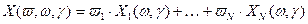есть ожидаемая доходность портфеля.
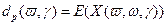. (2.1)
. Риск портфеля характеризуется дисперсией, либо среднеквадратичным отклонением соответствующей нечеткой случайной величины. В соответствии с рассматриваемым подходом эти характеристики являются функциями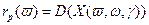 
, 
.
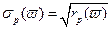