Взвешенная сумма нечетких случайных величин.
В контексте рассматриваемой проблемы портфельного анализа необходимо иметь соответствующие результаты для определения дисперсии и ожидаемого значение взвешенной суммы нечетких случайных величин. Итак, пусть имеем
Найдем математическое ожидание Лемма 1.4.1. Пусть
где Доказательство. Рассчитаем математическое ожидание. На основании леммы 1.1.2. и определения 1.1.18:
где Лемма доказана. Лемма 1.4.2. Дисперсия взвешенной суммы нечетких случайных величин находится по формуле:
Доказательство. Найдем Итак:
На основании теоремы 1.2.1 можно преобразовать полученное выражение следующим образом:
Проведем обратные преобразования, осуществим группировку слагаемых, воспользуемся свойством (2) из теоремы 1.2.1. Имеем:
Лемма доказана. Теорема 1.4.1. Пусть
Доказательство. Согласно лемме 1.4.2 дисперсия взвешенной суммы равна:
Обобщим лемму 1.3.1 и лемму 1.3.2 на случай
Теорема доказана.
|
несимметричных триангулярных нечетких случайных величин, 
- некоторые веса, такие, что 
. Будем рассматривать взвешенную сумму нечетких случайных величин: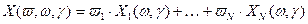
.
и дисперсию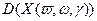 
для данной взвешенной суммы.
, 
,
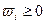. Тогда математическое ожидание взвешенной суммы нечетких случайных величин исчисляется по формуле:
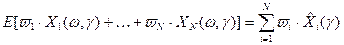, (1.4.1)
имеет распределение вида (1.3.2).
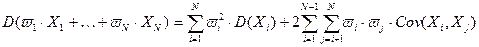(1.4.2)
, используя свойства (3),(4) из теоремы 1.2.1.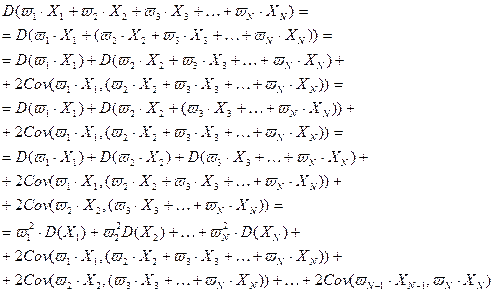
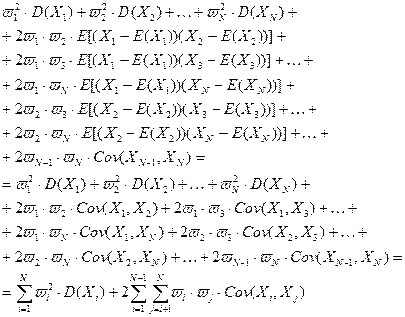
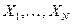вычисляется по формуле:
(1.3.1)
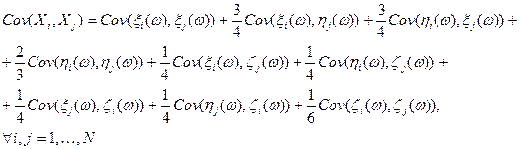Проведем соответствующие подстановки.
