Модель минимизации возможного риска при заданном уровне возможного дохода.
Модель имеет следующий вид:
где Данная задача может быть решена с помощью метода множителей Лагранжа. Сделаем некоторые преобразования. Пусть Тогда задача (2.4.1)-(2.4.2) принимает следующий вид:
Будем решать задачу (2.4.3)-(2.4.4) с помощью метода множителей Лагранжа. Функция Лагранжа в данном случае имеет вид:
Запишем в функции Лагранжа дисперсию в явном виде. В результате получаем:
Далее возьмем производные по всем
Присоединяя ограничение (2.4.2) мы приходим к системе уравнений:
где Запишем полученные уравнения в матричной форме с использованием следующих обозначений:
Тогда наша система примет следующий вид:
Предполагаем, что ковариационная матрица С невырождена ( Тогда: Подставляя это решение во второе и третье уравнения системы, получим уравнения для нахождения Итак, получили:
Решим эту систему с помощью метода Крамера. Имеем:
Далее подставив
|
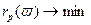, (2.4.1)
(2.4.2)
есть заданный уровень возможного дохода.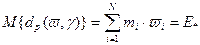
, где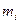 
- модальные значения 
.
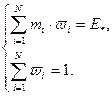(2.4.4)
.
.
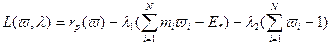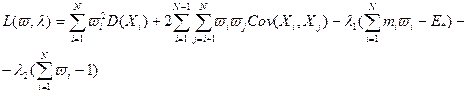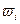, по 
и по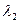 
. Получим следующие соотношения:
,
.
, 
.
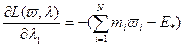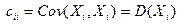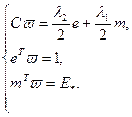
), следовательно, существует обратная матрица 
.
.
и 
.
,
.
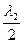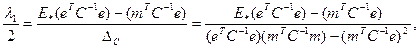
, получаем: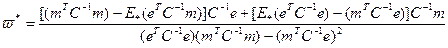
.
