Модель максимизации с заданной возможностью (необходимостью) ожидаемого дохода при фиксированном уровне возможного риска.
где Рассмотрим модель (2.3.1)-(2.3.2) в случае
В данной модели
Теорема 2.3.1. Пусть
Доказательство. Преобразуем первое ограничение системы (2.3.4). Имеем
на основании формулы представления [94] имеем
На основании обобщенной теоремы Вейерштрасса Нетрудно видеть, что получаемое неравенство
эквивалентно следующей системе неравенств:
Данные неравенства описывают
где Следствием последней системы неравенств является следующее неравенство:
Оно может быть записано в виде двух неравенств:
В результате эквивалентная модель критерия принимает вид:
Нетрудно видеть, что при
Таким образом, задача (2.3.3)-(2.3.4) имеет следующий эквивалентный детерминированный аналог:
Теорема доказана.
Преобразуя выражение для дисперсии согласно известной формуле (теорема 1.4.1), а также принимая
Если предположить, что параметры возможностного распределения являются независимыми случайными величинами, то
В результате наша задача сводится к следующей задаче математического программирования.
Уточним модель (2.3.7)-(2.3.8) для некоторых классов распределений. Пусть
Рассмотрим модель (2.3.1)-(2.3.2) в случае
В данной модели Теорема 2.3.1. Пусть
Доказательство. Построим эквивалентный детерминированный аналог. Действительно
Следовательно
Если
Таким образом, имеем в конечном итоге следующую эквивалентную модель
где Эквивалентная модель этого критерия может быть представлена в форме, не требующей использования уровневой переменной
Окончательно имеем следующий эквивалентный детерминированный аналог
Теорема доказана.
Преобразуя выражение для дисперсии согласно известной формуле (теорема 1.4.1), а также принимая
Если предположить, что параметры возможностного распределения являются независимыми случайными величинами, то
В результате наша задача сводится к следующей задаче математического программирования.
Уточним модель (2.3.15)-(2.3.16) для некоторых классов распределений. Пусть
|

 , (2.3.1)
, (2.3.1)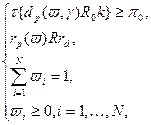 (2.3.2)
(2.3.2)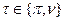 ,
,  есть четкое бинарное отношение:
есть четкое бинарное отношение: 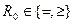 , k есть дополнительная уровневая переменная.
, k есть дополнительная уровневая переменная.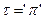 ,
,  . Получаем.
. Получаем.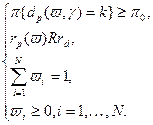 (2.3.4)
(2.3.4)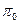 -уровень возможности.
-уровень возможности.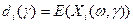 характеризуются квазивогнутыми, полунепрерывными сверху распределениями с ограниченными носителями. Тогда задача (2.3.3)-(2.3.4) имеет эквивалентный детерминированный аналог:
характеризуются квазивогнутыми, полунепрерывными сверху распределениями с ограниченными носителями. Тогда задача (2.3.3)-(2.3.4) имеет эквивалентный детерминированный аналог: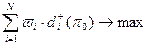 , (2.3.5)
, (2.3.5)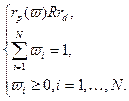 (2.3.6)
(2.3.6)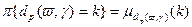 ,
,
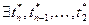 , на которых достигается супремумы (sup).
, на которых достигается супремумы (sup).

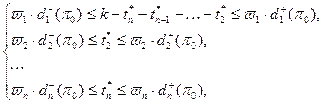
 ,
, 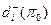 ,
,  есть правые и левые границы
есть правые и левые границы 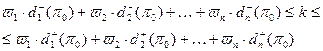

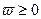 полученная модель критерия допускает эквивалентное представление:
полученная модель критерия допускает эквивалентное представление: , получаем:
, получаем: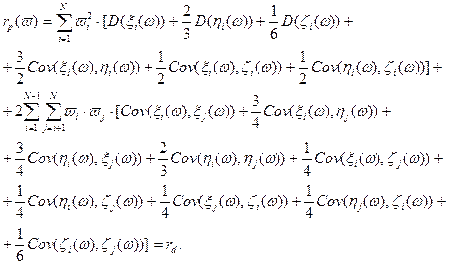
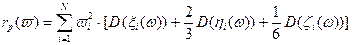 .
.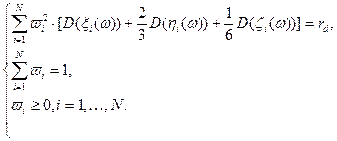 (2.3.8)
(2.3.8)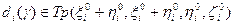 , тогда модель (2.3.7)-(2.3.8) будет преобразована следующим образом:
, тогда модель (2.3.7)-(2.3.8) будет преобразована следующим образом: , (2.3.9)
, (2.3.9)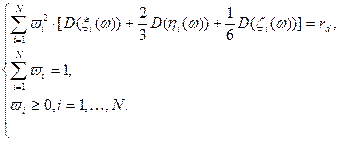 (2.3.10)
(2.3.10) . Имеем.
. Имеем.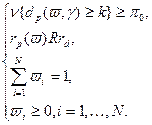 (2.3.12)
(2.3.12)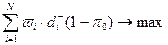 , (2.3.13)
, (2.3.13) .
.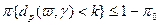 .
. является монотонной по нечетким параметрам и
является монотонной по нечетким параметрам и  .
.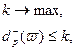
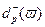 есть левая граница
есть левая граница 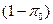 -уровневого множества нечеткой случайной величины, представляющей доходность инвестиционного портфеля.
-уровневого множества нечеткой случайной величины, представляющей доходность инвестиционного портфеля. :
: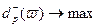 .
.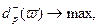
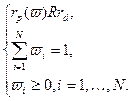
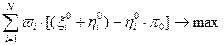 , (2.3.17)
, (2.3.17)


