Обобщение двумерного портфеля на случай нечетких случайных данных.
Обобщим двумерный портфель на случай нечетких случайных данных. Доли капитала, вкладываемые в первый и второй активы обозначим Будем рассматривать случай, когда доходности активов представляются нечеткими случайными величинами. При этом доходность портфеля будет также являться нечеткой случайной величиной:
а ожидаемая доходность портфеля будет нечеткой величиной:
где Рассматриваем случай, когда Не нарушая общности, можно считать, что Исследуем множество инвестиционных возможностей
В соответствии с результатами, полученными в первой главе:
Ввиду того, что параметр
Здесь Основываясь на [94] можно показать, что система (2.5.1) эквивалента следующей системе:
где Из соотношений (3.2.1)–(3.2.4) следует, что риск портфеля в конечном итоге определен на множестве значений доходности портфеля (замкнутом интервале) при каждом конечном фиксированном В результате мы можем констатировать, что множество инвестиционных возможностей есть «множественнозначная» кривая. При обозначениях
Решая систему (3.3) относительно переменных
Оптимальные портфели Имеем:
В пределе при На рисунке, приводимом ниже (рис.2.), представлено множество инвестиционных возможностей.
Рис.2. Множество инвестиционных возможностей
|

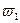 ,
,  соответственно.
соответственно. ,
, ,
, .
.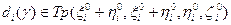 , где
, где  ,
,  ,
,  - ожидаемые значения случайных величин
- ожидаемые значения случайных величин  ,
,  ,
,  .
. ,
,  .
. , где
, где  есть риск портфеля:
есть риск портфеля: .
.
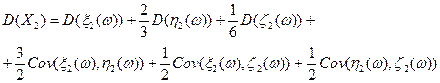

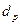 есть нечеткая величина, множество инвестиционных возможностей можно представить системой:
есть нечеткая величина, множество инвестиционных возможностей можно представить системой: (2.5.1)
(2.5.1)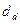 есть параметр со степенью возможности
есть параметр со степенью возможности  , представляющий
, представляющий 
 ,
,  ,
, 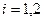 есть границы
есть границы  . Таким образом,
. Таким образом,  и
и 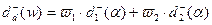 ,
, 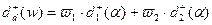 в соответствии с [3],
в соответствии с [3],  . Ясно, что эта кривая может быть построена с использованием «граничных» кривых, которые определяются посредством решения систем вида:
. Ясно, что эта кривая может быть построена с использованием «граничных» кривых, которые определяются посредством решения систем вида: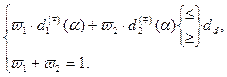 (3.3)
(3.3)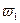 ,
,  в первом и во втором предельных случаях, после подстановки решений в (3.2.3), получаем две «граничные» параболы.
в первом и во втором предельных случаях, после подстановки решений в (3.2.3), получаем две «граничные» параболы.
 .
. могут быть получены путем решения уравнения
могут быть получены путем решения уравнения  .
. ,
, ,
, .
. можно считать, что
можно считать, что 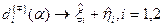 . И мы приходим, фактически, к классической модели портфельного анализа по Марковицу [85] с параметрами:
. И мы приходим, фактически, к классической модели портфельного анализа по Марковицу [85] с параметрами:  – вектор ожидаемых доходностей активов;
– вектор ожидаемых доходностей активов;  – ковариационная матрица,
– ковариационная матрица,  .
.



