Поняття степеневої середньої, формула розрахунку.

Степенева середня - це така величина, що розрахована за індивідуальними значеннями ознаки, піднесеними у ступінь К, і приведена до лінійних розмірів:

Залежно від ступеню К середня може бути гармонійною (К = -1), арифметичною (К = 1), геометричною (К = 0), квадратичною (К = 2), кубічною (К = 3), біквадратичною (К = 4). Кожна середня має визначені властивості і має свою сферу застосування.

Якщо для одного і того ж самого первинного ряду обчислити різні степеневі середні, то чим більший показник степені К, тим більше абсолютне значення середньої:

Це правило мажорантности степеневих середніх.

4. Порядкові середні

Порядкові середні розраховуються у ряді розподілу, впорядкованому за зростанням або зменшенням значення ознаки.

Модою (x_Mo) називається варіант значення ознаки, який найчастіше зустрічається в сукупності, або те значення ознаки, що відповідає максимальній точці теоретичної кривої розподілу.

В дискретному ряді мода - це варіант із найбільшою частотою. В інтервальному варіаційному ряді мода приблизно дорівнює центральному варіанту так називаного модального інтервалу. Її значення оцінюється за допомогою формули апроксимації (наближення):

,

 

де х ₀ - нижня межа модального інтервалу;

h_M0 - ширина модального інтервалу;

f _M0 - абсолютна частота модального інтервалу;

f _M0-1 - абсолютна частота інтервалу перед модальним;

f _M0+1 - абсолютна частота інтервалу наступного за модальним.

Квантилі – це значення ознаки, які поділяють впорядкований ряд на певну кількість рівних частин. Наприклад:

· медіана – на 2 частини;

· терцилі – на 3 частини;

· квартилі – на 4 частини;

· квінтилі – на 5 частин;

· децилі – на 10 частин;

· процентилі – на 100 частин.

Медіана (x_Me) - це величина ознаки, що поділяє чисельність впорядкованого варіаційного ряду на 2 рівні частини. Одна частина значення варіюючої ознаки менша за медіану, а інша частина - більша. Для впорядкованого ряду з непарним числом членів медіаною є варіанта, розташована в центрі ряду, а у випадку з парним числом членів медіаною буде середня арифметична з двох суміжних центральних варіант.

В інтервальному варіаційному ряді порядок знаходження медіани наступний:

а) впорядковуємо індивідуальні значення ознаки за збільшенням (зменшенням) значення ознаки – за ранжиром;

б) визначаємо для даного ряду значення кумулятивної функції для частот, тобто нагромаджені частоти для кожного інтервалу значень;

в) за даними про нагромаджені частоти знаходимо медіанний інтервал.

Медіана поділяє чисельність ряду навпіл, отже, вона знаходиться в тому інтервалі, в якому значення кумулятивної функції складає половину або більше половини всієї суми частот, а значення кумулятивної функції для попереднього інтервалу менше половини чисельності сукупності.

Якщо припускати, що всередині медіанного інтервалу наростання або зменшення досліджуваної ознаки відбувається рівномірно, тоді формула апроксимації для медіани в інтервальному ряді розподілу буде мати наступний вигляд:

,

де х ₀ - нижня межа медіанного інтервалу;

h_me - ширина медіанного інтервалу;

Σ f /2 - полусума частот ряду (обсягу ряду);

F_Mе-1 – сума частот всіх інтервалів перед медіанним;

f _Mе - частота медіанного інтервалу.

Квартилі (Q) - це значення ознаки, що поділяють впорядкований ряд на 4 рівні частини. Розрізняють нижній квартиль Q1, медіану Ме і верхній квартиль Q3. Нижній та верхній квартилі розраховують за формулами:

де x _min - мінімальні межі квартильних інтервалів;

h - ширина інтервалу ряду розподілу;

; - суми частот всіх інтервалів перед квартильним;

f _Q1; f _Q3 - частоти квартильних інтервалів.

Децилі (D) – варіанти, які поділяють впорядкований ряд на 10 рівних частин. Так, перший та другий децилі можна обчислити за формулами:

,

де x _min - мінімальні межі децильних інтервалів;

h - ширина інтервалу ряду розподілу;

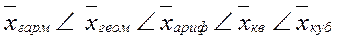
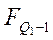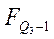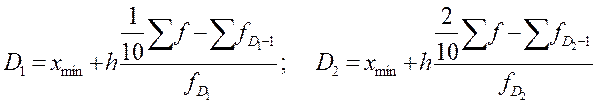; - суми частот всіх інтервалів перед децильним;

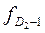; - частоти децильних інтервалів.