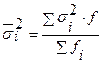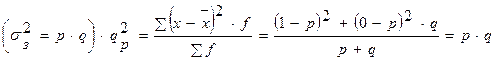Показники варіації
Поняття варіації ознаки, показники варіації, дисперсія альтернативної ознаки. Спрощений спосіб розрахунку дисперсії. Види дисперсій у сукупності, розбитої на групи, правило додавання дисперсій Здатність ознаки приймати різні значення називають варіацією ознаки. Для вимір варіації ознаки використовують різні узагальнюючі показники - абсолютні та відносні. 1. Розмах варіації - це різниця максимального і мінімального значень ознаки: R = х max - х min. 2. Середнє лінійне відхилення - це середня з абсолютних значень відхилень ознаки від своєї середньої:
3. Середня з квадратів відхилень значень ознаки від середньої, тобто дисперсія:
Дисперсія як різниця між середнім квадратом та квадратом середньої:
або
Дисперсія можна обчислювати методом умовних моментів. Момент розподілу – це середня m відхилень значень ознаки від довільної величини А: якщо А = 0, тоді момент називається початковим; якщо А = В залежності від показника степені К, в який піднесені відхилення (х – А)к, моменти називаються моментами 1-го, 2-го и т.д. порядків.
Порядок розрахунку дисперсії методом умовних моментів („відліку від умовного нуля”): 1. Вибір умовного нуля С; 2. Перетворення фактичних значень ознаки х в спрощені х´; через відлік від умовного нуля С та зменшення в d раз: 3. Розрахунок 1-го умовного моменту: 4. Розрахунок 2-го умовного моменту: 5. Розрахунок початкового моменту 1-го порядку:
6. Дисперсія:
Середнє квадратичне відхилення розраховується з даних про дисперсію
Відносні величини варіації 1. Коефіцієнт осциляції відображає відносні коливання крайніх значень ознаки навколо середньої: 2. Відносне лінійне відхилення: 3. Коефіцієнт варіації: 4. Коефіцієнт асиметрії:
Види дисперсій та правило додавання дисперсій
А) Загальна дисперсія: де
Б) Міжгрупова дисперсія: де
В) Середня внутрішньогруповых дисперсій Загальна дисперсія дорівнює сумі з міжгрупової дисперсії та середньої внутрішньогрупової дисперсії: Дисперсія альтернативної ознаки дорівнює добутку частки одиниць, яким притаманна дана досліджувана ознака та частки одиниць, яким не притаманна дана досліджувана ознака.
|

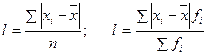
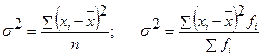
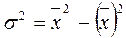
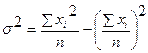 - проста
- проста - зважена
- зважена , тоді моменти – центральними; якщо А = С, тоді моменти – умовними.
, тоді моменти – центральними; якщо А = С, тоді моменти – умовними.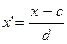



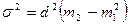
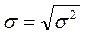

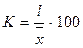

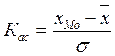
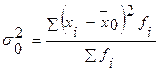
 - загальна середня усієї сукупності
- загальна середня усієї сукупності ,
, - середня окремих груп
- середня окремих груп