Властивості середньої арифметичної

Середня арифметична величина володіє рядом властивостей, що дозволяють прискорити розрахунок.

1) Вона не змінюється, якщо ваги усіх варіантів помножити або розділити на одне і те саме число.

2) Якщо всі значення ознаки однакові, тоді середня дорівнює цій же величині.

3) Середні суми або різниці дорівнюють сумі або різниці середніх:

4) Якщо з усіх значень x_i відняти постійну величину А, то середня зменшується на це значення.

5) Якщо всі значення зменшити в d раз (x_i/d), то середня зменшиться в d раз.

6) Сума відхилень значення ознаки дорівнює 0.

7) Сума квадратів відхилень

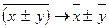
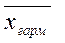2. Середня гармонійна визначається як величина обернена до середньої арифметичної з обернених величин. Використовується для осереднення обернених індивідуальних значень ознак шляхом підсумовування. Застосовується у випадках, коли осереднювала ознака є відношенням між логічно пов’язаними величинами, і чисельник дробу логічної формули відомий з наявних даних, а знаменник – ні.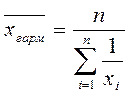

Для не згрупованих даних розраховують середню гармонійну просту:

Якщо статистичні дані представлені у вигляді рядів або розподілу (згруповані), тоді середня обчислюється як середня гармонійна зважена:

- де сумарне значення ознаки.

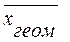3. Середня геометрична обчислюється як корінь n-го ступеню з добутку n множників. Використовується тоді, коли визначальна властивість сукупності формується як добуток індивідуальних значень ознаки. Найчастіше застосовується при дослідженні інтенсивності розвитку: обчисленні середньої частки відносних змін (середні темпи зростання, приросту) та побудові індексів.

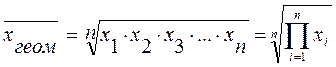- проста, для не згрупованих даних;

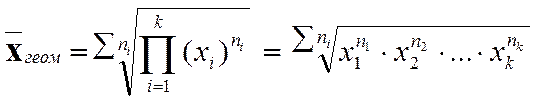- зважена, для згрупованих даних, де ∑n_i = n часовий інтервал.