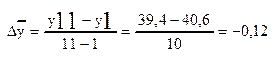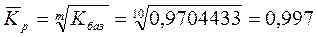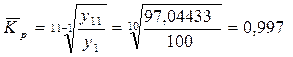Вирівнювання рядів динаміки
Вирівнювання рядів динаміки проводять одним зі способів: а) Механічне вирівнювання полягає в укрупненні інтервалу часу і розрахунку середньої хронологічної б) Аналітичне вирівнювання - це опис тенденцій за допомогою підбору адекватної моделі, що представляє математичну функцію залежності середнього рівня від часу: де a 0 та а 1 - параметри рівняння, які розраховуються на основі фактичних даних методом найменших квадратів
Вирівнювання можна проводити за параболою 2-го порядку:
Коли для вирівнювання застосовується показникова функція, тоді рівняння взаємозв’язку: Подальший розв’язок аналогічний вирівнюванню за прямою. При виборі моделі можна керуватися наступними правилами 1) Якщо абсолютні прирости коливаються навколо постійної величини, доцільно використовувати модель прямої: Δy = уi - уi-1; а0 - база; а1t - приріст. 2) Якщо прирости приростів (Δ у 2 – Δ у 1), тобто прискорення, коливається навколо постійної величини, тоді доцільно використовувати параболу 2-го порядку: 3) У випадку приблизно однакових темпів зростання використовують модель показникової функції: ПРИКЛАД 1.
Середня хронологічна:
Похідні показники ряду динаміки:
Взаємозв’язок ланцюгових і базових коефіцієнтів зростання: 1. Добуток послідовних ланцюгових коефіцієнтів дорівнює базовому коефіцієнту:
2. Ланцюговий індекс можна отримати з відношення базового коефіцієнта за досліджуваний період до базового коефіцієнта за попередній період.
Середній абсолютний приріст:
Середній річний коефіцієнт зростання обчислюється за формулою середньої геометричної: 1) 2) 3)
|

 За рівнянням прямої:
За рівнянням прямої: 
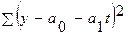
 - умовний час, прийнятий від певної бази.
- умовний час, прийнятий від певної бази. , а0, а1, а2 - параметри, які визначають за допомогою системи рівнянь:
, а0, а1, а2 - параметри, які визначають за допомогою системи рівнянь: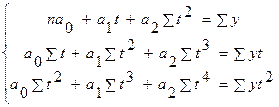 - якщо Σ t = 0, тоді Σ t 3 = 0
- якщо Σ t = 0, тоді Σ t 3 = 0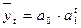 Для знаходження параметрів такої моделі логарифмують праву та ліву частини рівняння:
Для знаходження параметрів такої моделі логарифмують праву та ліву частини рівняння: 
 ,: де а0 - база; а1t - приріст; а2t2 - прискорення
,: де а0 - база; а1t - приріст; а2t2 - прискорення - середній коефіцієнт зростання.
- середній коефіцієнт зростання.
 - абсолютний приріст, ланцюговий.
- абсолютний приріст, ланцюговий.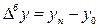 - абсолютний приріст, базовий.
- абсолютний приріст, базовий.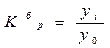 - коефіцієнт зростання, базовий.
- коефіцієнт зростання, базовий.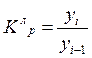 - коефіцієнт зростання, ланцюговий.
- коефіцієнт зростання, ланцюговий.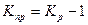 - коефіцієнт приросту
- коефіцієнт приросту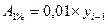 - абсолютне значення одного відсотка приросту.
- абсолютне значення одного відсотка приросту.

 и т. д.
и т. д.
 и т. д.
и т. д.