Операторная передаточная функцияВажную роль в методах анализа и синтеза ЭЦ играет операторнаяпередаточная функция H(p), равная отношению изображения реакции цепи и изображению воздействия при нулевых начальных условиях. Различают следующие виды передаточных функций: Операторная передаточная функция представляет собой дробно-рациональную функцию с вещественными коэффициентами Степени полиномов числителя и знаменателя зависят от числа реактивных элементов цепи и её схемы. Устойчивыми называются ЭЦ, у которых при произвольных начальных условиях свободные колебания стремятся к нулю с неограниченным ростом времени, т.е. переходные процессы будут затухающими. Цепь будет устойчивой, если все полюсы передаточной функции (корни уравнения N(p)=0) располагаются в левой полуплоскости комплексной переменной р. Они могут быть вещественными или комплексно- сопряженными. Для этого необходимо, чтобы полином N(p) содержал вещественные коэффициенты, т.е. являлся полиномом Гурвица.
Рис. 7.3. Расположение полюсов устойчивой цепи в случае а) действительных корней; б) комплексно- сопряженных корней. Зная операторную передаточную функцию, можно найти изображение реакции, а по нему и реакцию цепи на заданное воздействие. Пример: Определить u2(t) цепи рис. 7.4а
Рис. 7.4. Исходная схема а) и её операторная схема замещения б). По таблице определим оригинал u2(t) 7.7. Вопросы для самоконтроля к лекции 7 1. Какова сущность операторного метода расчёта переходных процессов? 2. Что такое оригинал функции? 3. Что такое изображение функции? 4. Разберите основные свойства преобразования Лапласа. 5. Как составляются эквивалентные операторные схемы? 6. Как можно найти оригинал функции по известному изображению? 7. Какова последовательность расчёта электрической цепи операторным методом? 8. Дайте определение операторной передаточной функции. Каковы её свойства? 9. Разберите решения задач 9.1, 9.4 из [4] 10. Решите задачи 9.2, 9.3 из [4]. Литература: [1] с. 218-248; [2] с. 121-127; [3] с. 219-237; [4] с. 251-257; [5] с. 381-391. Лекция 8. Анализ ЛЭЦ при импульсных воздействиях
|
; 
; 
; 
.
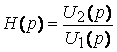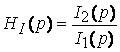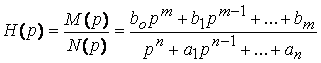. (7.12)
;
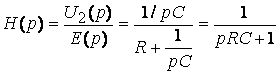