Временной метод анализа ЛЭЦ
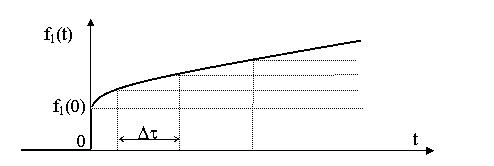
Временной метод анализа применяется для определения реакции цепи на сложное воздействие при нулевых начальных условиях. Использование понятий переходной и импульсной характеристик позволяет свести расчёт реакции цепи на сложное воздействие к определению реакции на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходное воздействие. При этом результирующая реакция находится как сумма реакций цепи на элементарные воздействия. Если известна переходная характеристика цепи, то сложное воздействие f1(t) аппроксимируется ступенчатыми функциями, возникающими через равные промежутки времени Dt (рис. 8.3)
Рис. 8.3 Представление сложной функции ступенчатой функцией. В этом случае реакция цепи определяется при помощи интеграла Дюамеля. Если известна или легко определяется импульсная характеристика цепи, то сложное воздействие f1(t) аппроксимируется последовательностью прямоугольных импульсов (рис. 8.4)
Рис. 8.4. Представление сложной функции последовательностью прямоугольных импульсов. В этом случае реакция цепи f2(t) определяется при помощи интеграла наложения. Расчёт ЭЦ временным методом производится в следующем порядке: 1. Определение переходной h(t) или импульсной g(t) характеристики цепи. 2. Определение переходной h(t-t) или импульсной g(t-t) характеристики путём замены t на t-t. 3. Определение производной от входного напряжения u1(t) по времени. 4. Определение реакции с помощью интеграла Дюамеля или наложения. Пример: Определить u2(t) цепи рис. 8.5.
Рис. 8.5. Исходная схема а) и вид воздействия б). u1(0)=U; При 0£ t £ tU При t ³ tU
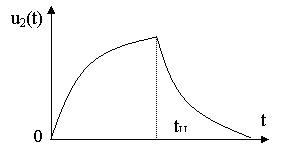
Рис. 8.6. Временная зависимость выходного напряжения.
|

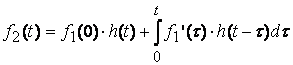 (8.5)
(8.5)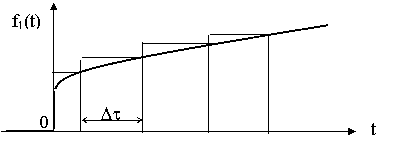
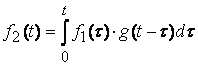 . (8.6)
. (8.6)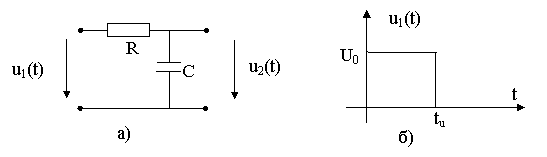
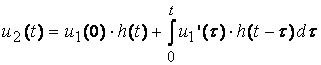 ;
;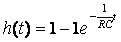 ; u1’(t)=U0’=0;
; u1’(t)=U0’=0;
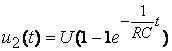 .
.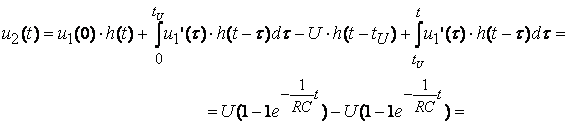
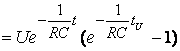 .
.