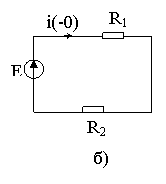
Определение оригинала функции по его изображениюСуществуют три способа определения оригинала искомой функции по его изображению: 1) с помощью обратного преобразования Лапласа; 2) с помощью таблиц; 3) по теореме разложения. Если изображение F(p) получено в виде рациональной дроби 1) корни вещественны и различны F2(p)=0; n -число корней; 2) при наличии нулевого корня Пример: Определить оригинал функции p1= -2; p2=0 F1(0)=3; F3(0)=2; F1(p1)=-2+3=1; F3’(p1)=2 7.5. Порядок расчёта переходных процессов операторным методом Расчёт производится в следующем порядке: 1. Определение независимых начальных условий 2. Составление эквивалентной операторной схемы цепи после коммутации 3. С помощью любого из методов расчёта определить изображение искомых величин 4. По полученному изображению определить оригинал искомой функции Пример: Определить переходной ток в цепи рис. 7.2а операторным методом.
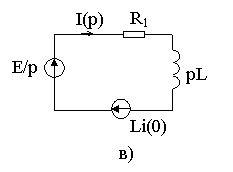
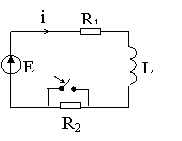
Рис. 7.2. Независимые начальные условия определяются по схеме рис. 7.2б. Эквивалентная операторная схема приведена на рис. 7.2в По закону Ома Определим оригинал тока: 1 способ - с помощью таблицы «оригинал-изображение» По таблице 2 способ - по теореме разложения (7.11) F1(0)=E; F3(0)=R1; F3’(p)=L;
|
, то оригинал определяется по теореме разложения. В зависимости от вида корней уравнения F2(p)=0, существуют следующие виды записи теоремы разложения:
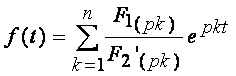, где рк – корни функции (7.10)
.
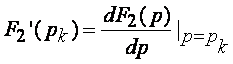(7.11)
.
; 
.
.
; 
;
,
.
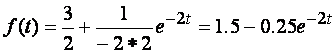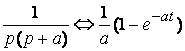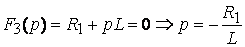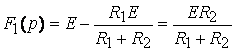