По закону Ома ток линии 3 страница
2) рассчитать емкость С Р, необходимую для настройки цепи рис. 5.4 в резонанс токов, вычислить в резонансном режиме токи I, I K, IC, мощности Р и Таблица 5.1
Порядок выполнения работы 1. Собрать электрическую цепь по схеме рис. 5.3.
  
  


 
                  
 
    
   
     

2. Установить на входе цепи напряжение U согласно варианту задания для резонанса напряжений. Изменяя емкость конденсаторов, получить резонанс напряжений (при этом показание фазометра j = 0). Изменяя сопротивление реостата R р, установить ток I, равный расчетному в табл. 5.2 при С = С р. Сравнить напряжения U K и UC с расчетными значениями. После этого произвести три измерения при С < С Р и три измерения при С > С Р. Результаты измерений записать в табл. 5.2. 3. По результатам измерений и параметрам элементов R и L рассчитать и записать в табл. 5.2 активную мощность Р, реактивную мощность Q, активную UR и реактивную UL составляющие напряжения U K, емкость конденсаторов С.
Таблица 5.2
4. Построить в масштабе две векторные диаграммы для случаев: С < С Р и С = С Р. На диаграммах показать вектор тока 5. Построить совмещенные графики зависимостей I, UL, UC, j = f (C). 6. Собрать электрическую цепь по схеме рис. 5.4.
   
             
 

 
      



7. Установить на входе цепи напряжение U согласно варианту задания для резонанса токов (табл. 5.1). Изменяя сопротивление реостата R р при отключенной батарее конденсаторов, установить ток I К, равный расчетному Таблица 5.3
8. По результатам измерений и параметрам элементов рассчитать и записать в табл. 5.3 активную мощность Р, реактивные мощности QL, QC, Q = QL – QC и емкость конденсаторов С. 9. Построить в масштабе две векторные диаграммы для случаев: С < С Р и С = С Р. На диаграммах показать векторы напряжения 10. Построить совмещенные графики зависимостей I, cos j, Q = f (C).
Содержание отчета 1. Цель работы. 2. Схемы электрических цепей для исследования резонансов (рис. 5.3, 5.4). 3. Исходные данные и полный расчет предварительного задания к эксперименту. 4. Таблицы вычислений и измерений, четыре векторные диаграммы. 5. Графики зависимостей I, UL, UC, j = f (C) для последовательной цепи и I, cosj, Q = f (C) для параллельной цепи. 6. Выводы об энергетических процессах и о практическом использовании резонансов в технике. Контрольные вопросы 1. Каковы условия возникновения резонанса напряжений (токов) и как его можно получить? 2. По каким признакам можно убедиться, что в цепи наступил резонанс напряжений (токов)? 3. Должны ли быть равны при резонансе напряжения UК и UC? 4. Как изменятся ток I и мощность Р, если в последовательной цепи, настроенной в резонанс, увеличить сопротивление R в два раза? 5. Как изменятся мощности Р и Q в последовательной (параллельной) цепи, если после настройки в резонанс увеличить частоту источника? 6. Сохранится ли в цепях рис. 5.3, 5.4 резонанс, если после настройки в резонанс увеличить сопротивление R? 7. Как строятся векторные диаграммы для исследованных цепей? 8. Какие энергетические явления происходят при резонансах? 9. Дайте анализ зависимостей I, UL, UC, j = f (C); I, cosj, Q = f (C). 10. Каково практическое использование резонансных явлений в технике? 11. Каковы устройство, принцип действия и условные обозначения приборов электромагнитной и электродинамической систем?
Лабораторная работа 1.6 КОМПЕНСАЦИЯ РЕАКТИВНОЙ МОЩНОСТИ Цель работы: исследование влияния компенсации реактивной мощности потребителя электроэнергии на технико-экономические показатели электропередачи. Общие сведения Большинство современных потребителей электроэнергии переменного тока наряду с активной мощностью Р потребляет из сети реактивную (индуктивную) мощность QL. Это обусловлено тем, что электродвигатели, трансформаторы и другие электротехнические устройства содержат обмотки, связанные с переменными магнитными полями, т.е. помимо активного сопротивления обладают индуктивностью. Потери активной мощности в линии электропередачи (ЛЭП), питающей потребитель и имеющей сопротивление R л,
Из этого выражения видно, что потери активной мощности в линии можно разделить на две составляющие: потери от передачи активной мощности Р и потери от передачи реактивной мощности Q. Отношение Q / Р = tgj называют коэффициентом реактивной мощности (cosj = P / S – коэффициент активной мощности). Естественный tgj промышленных предприятий (без установки специальных компенсирующих устройств) обычно находится в пределах Кроме того, загрузка генераторов, трансформаторов и ЛЭП реактивной мощностью требует повышения установленной мощности генераторов и трансформаторов, а также сечения проводов ЛЭП. Генераторы и трансформаторы рассчитывают на определенный номинальный ток I ном и номинальную мощность Потребление реактивной мощности снижают с помощью организационно-технических мероприятий и путем компенсации реактивной мощности. К организационно-техническим мероприятиям относятся: а) упорядочение технологических процессов с целью повышения загрузки оборудования и асинхронных двигателей, так как при малой загрузке коэффициент реактивной мощности tgj = Q / Р резко возрастает; б) замена малозагруженных асинхронных двигателей и трансформаторов двигателями и трансформаторами меньшей мощности; в) ограничение времени работы двигателей в режиме холостого хода; г) применение, где это возможно, вместо асинхронных двигателей синхронных, работающих с cosj, близким к 1, либо с потреблением емкостной мощности. Как правило, одних организационно-технических мероприятий оказывается недостаточно и дальнейшее снижение Q осуществляют путем компенсации части или всей реактивной мощности потребителя. Для этого параллельно потребителю подключают батареи конденсаторов (БК) или синхронные двигатели, работающие в режиме потребления емкостной мощности (рис. 6.1а).
Ток потребителя Умножив это равенство на U, получим уравнение для мощностей Q = QL – QC или Q + QC = QL. Последнее соотношение означает, что генератор, вырабатывающий реактивную мощность Q, и БК мощностью QC совместно покрывают реактивную мощность потребителя QL. Следовательно, БК по существу является местным источником реактивной мощности. Физическое объяснение роли конденсаторов в процессе компенсации реактивной мощности состоит в следующем. Генерирование и потребление реактивной мощности представляет периодический обмен энергией между источником и потребителем. Емкость конденсаторов С и индуктивность потребителя L образуют колебательный контур (рис. 6.1а), в котором осуществляется обмен энергией между С и L. Принимая на себя основную часть указанного колебательного процесса, БК разгружает от него генератор и ЛЭП. Целесообразная степень компенсации реактивной мощности определяется экономическими соображениями. Для небольших предприятий часто экономически выгодна полная компенсация реактивной мощности Мощность БК, необходимая для компенсации реактивной мощности, определяется по формуле QC = Q п– Q = P (tgjп – tgj ), где Р – активная мощность потребителя; Q п – естественная реактивная мощность потребителя; Q – заданное значение реактивной мощности, поступающей из энергосистемы; tgjп,tgj – естественный и требуемый коэффициенты реактивной мощности. Предварительное задание к эксперименту Приемник электроэнергии имеет полное сопротивление Z п = 70 Ом, коэффициент реактивной мощности tgjп = 2,05 ( jп = 64°). Для компенсации реактивной мощности приемника параллельно ему включена батарея конденсаторов С (рис. 6.2).
|






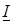 и векторы напряжений U, U К, U C, U R, U L.
и векторы напряжений U, U К, U C, U R, U L.





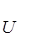 и токов
и токов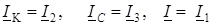 .
.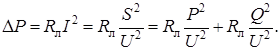
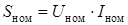 , превышать которые нельзя:
, превышать которые нельзя:  . При данной активной мощности потребителя Р возрастание Q требует установки генераторов и трансформаторов большей номинальной мощности S ном и сооружения ЛЭП с большей пропускной способностью (большим сечением проводов). В результате капитальные затраты на сооружение электростанций, трансформаторных подстанций и ЛЭП, а также текущие расходы на их обслуживание возрастают. Полная или частичная разгрузка электростанций и ЛЭП от реактивной мощности существенно повышает экономичность систем электроснабжения.
. При данной активной мощности потребителя Р возрастание Q требует установки генераторов и трансформаторов большей номинальной мощности S ном и сооружения ЛЭП с большей пропускной способностью (большим сечением проводов). В результате капитальные затраты на сооружение электростанций, трансформаторных подстанций и ЛЭП, а также текущие расходы на их обслуживание возрастают. Полная или частичная разгрузка электростанций и ЛЭП от реактивной мощности существенно повышает экономичность систем электроснабжения.
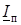 имеет активную
имеет активную 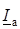 и индуктивную
и индуктивную 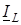 составляющие (рис. 6.1). Подключение БК приводит к появлению емкостного тока
составляющие (рис. 6.1). Подключение БК приводит к появлению емкостного тока 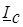 , который компенсирует реактивную составляющую тока
, который компенсирует реактивную составляющую тока 


