По закону Ома ток линии 5 страница
Кривые изменения u c и i в функции времени даны на рис. 8.3. Они представляют собой затухающие синусоидальные колебания с угловой частотой свободных колебаний
Кривые uc и i касаются огибающих Сопротивление R оказывает существенное влияние на скорость колебательного разряда конденсатора. Кроме того, по мере увеличения R уменьшается частота свободных колебаний wсв и увеличивается их период Т св. Когда В настоящей работе процесс разряда конденсатора исследуется с помощью электронного осциллографа, на экране которого наблюдаются кривые напряжения и тока конденсатора. Для этой цели необходимо, чтобы разряд конденсатора периодически повторялся во времени с определенной частотой, что достигается с помощью быстродействующего поляризованного реле РП
  
      
 
  
При подключении обмотки реле к источнику переменного напряжения средний контакт начинает вибрировать с частотой сети ( Предварительное задание к эксперименту При заданных в табл. 8.1 параметрах цепи R и C 1) рассчитать постоянную времени t цепи разряда конденсатора через резистор (рис. 8.1); 2) вычислить критическое сопротивление R кр цепи рис. 8.2 а при разряде конденсатора на катушку индуктивности с параметрами 3)определить частоту свободных колебаний wсв и коэффициент затухания d колебательного контура R, L, C. Полученные значения записать в табл. 8.2. Таблица 8.1
Порядок выполнения эксперимента 1. Cобрать электрическую цепь по схеме рис. 8.4 для разряда конденсатора через резистор R. 2. Подключить питание осциллографа и после его пятиминутного прогрева подать на вход осциллографа напряжение конденсатора (зажимы 1,3). Получить на экране кривую 3. По осциллограмме пункта 2 определить постоянную времени t, значение t записать в табл. 8.2 и сравнить с расчетной величиной. Таблица 8.2
4. Подготовить электрическую цепь по схеме рис. 8.4 для разряда конденсатора на катушку индуктивности и резистор R. 5. Получить на экране осциллографа кривую 6. Установить величины R и C по данным табл. 8.1 и зарисовать с экрана осциллографа кривую 7. Подать на вход осциллографа кривую тока i (t) (зажимы 2,3), зарисовать ее при прежних значениях R и C, совместив с ранее полученной кривой 8. По осциллограммам пунктов 6 и 7 определить частоту свободных колебаний wсв и коэффициент затухания d, значения записать в табл. 8.2. Выполнить моделирование переходных процессов на ПЭВМ (программа «РРRLС»). Содержание отчета 1. Цель работы. 2. Схема электрической цепи (рис. 8.4). 3. Таблицы вычислений и измерений, расчетные формулы. 4. Осциллограммы разрядного напряжения 5. Выводы о влиянии параметров R, C на характер и длительность переходных процессов в исследованных цепях. Контрольные вопросы 1. Что называется переходным процессом? Приведите примеры. 2. Как выполняется расчет переходных процессов? 3. Сформулируйте законы коммутации. Поясните их на примере исследованных цепей. 4. Каково влияние параметров цепи R, L, C на длительность процесса разряда конденсатора, частоту свободных колебаний и их период? 5. Что такое критическое сопротивление? 6. Что такое постоянная времени и коэффициент затухания цепей R, C и R, L, C? Как они определяются по параметрам цепи и по осциллограммам? 7. Каковы энергетические процессы в цепи R, L, C при апериодическом и колебательном разрядах конденсатора? 8. Как получены на экране электронного осциллографа кривые разрядного тока и напряжения? Лабораторная работа 1.9 ОДНОФАЗНЫЙ ИНДУКЦИОННЫЙ СЧЕТЧИК АКТИВНОЙ ЭНЕРГИИ
Цель работы: ознакомление с устройством, принципом действия и способом поверки однофазного счетчика. Общие сведения Измерение активной энергии в цепях переменного тока проводится с помощью интегрирующих электроизмерительных приборов - электрических счетчиков. Технические требования к ним регламентированы ГОСТ 6570 -96. В счетчиках используется индукционный измерительный механизм, устройство которого упрощенно показано на рис. 9.1, где 1 – трехстрежневой магнитопровод с обмоткой напряжения, 2 – П-образный магнитопровод с токовой обмоткой, 3 – алюминиевый диск, укрепленный на подвижной оси, 4 – противополюс, 5 – постоянный магнит. Ток в обмотке напряжения IU создает магнитный поток Ф, часть которого замыкается через боковые стержни (Ф L), а часть через диск 3 и противополюс 4 – это рабочий поток Ф U, отстающий от тока IU на угол a U (рис. 9.2).
                                                                    
Для учета счетчиком только активной энергии необходимо, чтобы вращающий момент был пропорционален активной мощности нагрузки М = С 1 P = C 1 UI cosj. Из-за наличия больших воздушных зазоров в сердечниках поток Ф I пропорционален току I, а поток Ф U – напряжению U. Следовательно, счетчик учитывает активную энергию, если выполнено фазное условие siny = cosjилиy + j = 900. Для обеспечения равномерной угловой скорости диска создают тормозной момент М Т с помощью постоянного магнита 5. При вращении диска в магнитном поле постоянного магнита в диске наводятся вихревые токи и в результате их взаимодействия с полем постоянного магнита возникает тормозной момент, пропорциональный скорости вращения диска n,
|
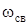и коэффициентом затухания d, зависящими от параметров контура R, L, C.
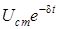и 
(и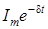зображены пунктиром), когда синус равен единице. При 
ордината огибающей в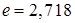 
раз меньше начального значения огибающей. Поэтому величину 
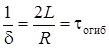называют постоянной времени колебательного контура.
; 
; 
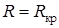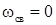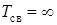, что соответствует апериодическому разряду.
; 
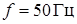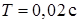), периодически замыкая контакты реле. При этом в левом положении контакта конденсатор заряжается до напряжения U 0, в правом – разряжается. Пренебрегая временем переключения контактов, можно считать, что процесс разряда конденсатора, наблюдаемый на экране осциллографа, длится 
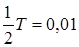секунды.
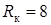Ом и 
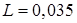Гн;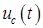
. Поочередно изменяя величины R и C, проанализировать, как изменяется форма кривой 
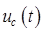и, изменяя сопротивление R, затем емкость С, проследить, как изменяется процесс разряда конденсатора. Установить значение емкости С в соответствии с данными табл. 8.1 и, регулируя сопротивление R, по форме кривой 
.
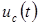