По закону Ома ток линии 6 страница
М Т = С 2 n. Равновесие устанавливается при М = М Т или C 1 P = C 2 n. За время t диск сделает N = nt оборотов, а нагрузка потребит энергию C 1 Pt = C 2 nt или C 1 W = C 2 N. Таким образом, число оборотов диска N пропорционально учитываемой счетчиком энергии. Коэффициент пропорциональности Число оборотов диска, приходящееся на 1 кВт×ч (N 0), называют передаточным числом. Оно указывается на счетчике. Например: 1 кВт×ч – 2500 оборотов диска. Величина, обратная передаточному числу N 0, определяет номинальную постоянную счетчика С ном. При работе счетчика в опорах диска и в счетном механизме возникают силы трения, зависящие от скорости вращения. Обусловленный ими тормозной момент трения вносит погрешность в показания счетчика. Для компенсации момента трения в счетчике предусмотрена специальная магнитная система, создающая дополнительный вращающий момент, не зависящий от тока нагрузки. Этот компенсационный момент пропорционален квадрату напряжения. При неправильной регулировке счетчика компенсационный момент может превысить момент трения и диск счетчика будет вращаться даже при отключенной нагрузке. Это явление называют самоходом. Если компенсационный момент меньше момента трения, то счетчик не будет работать при малых нагрузках. Минимальная нагрузка Р min, при которой диск счетчика непрерывно вращается, определяет порог чувствительности (чувствительность)
Целью поверки счетчика является определение его погрешности, чувствительности и самохода. Наиболее точный метод
с действительной энергией, подсчитанной по образцовому ваттметру и секундомеру W д= PW × t. В результате поверки определяют относительную погрешность счетчика
При маркировке счетчика указывают: тип, единицы измерения электрической энергии, номинальное напряжение, номинальный и максимальный ток (10 –40 (А) или 10(40) А), номинальную частоту сети, постоянную счетчика, класс точности прибора. По точности счетчики активной энергии подразделяются на классы 1,0; 2,0; 2,5. В отличие от электромеханических приборов других систем, класс точности счетчиков определяется не приведенной, а относительной погрешностью. Допустимые погрешности для счетчиков класса 2,5 приведены в табл. 9.1. Таблица 9.1
Предварительное задание к эксперименту Для электрической цепи по схеме рис. 9.3 вычислить показания амперметра, ваттметра и определить число оборотов N диска счетчика за 5 минут работы установки, если вольтметр показывает 220 В, передаточное число счетчика N 0 = 1200, величины R и С заданы в табл. 9.2. Таблица 9.2
Результаты расчетов записать в табл. 9.3. Таблица 9.3
Порядок выполнения эксперимента 1. По паспортным данным счетчика определить номинальную постоянную С ном и номинальную мощность S ном = U ном. I ном. 2. Собрать электрическую цепь по схеме рис. 9.3.
3. Установить на зажимах цепи напряжение U = 220 В и заданные значения R, C. Измерить ток и зафиксировать число оборотов счетчика N за пять минут его работы. результаты измерений записать в табл. 9.3 и сравнить их с расчетными значениями. 4. Повторить проведенные измерения при отключенной емкости С = 0. Проанализировать полученные результаты. 5. Проверить счетчик на отсутствие самохода. Для этого при отключенной нагрузке повысить напряжение на 10% сверх номинального. Диск счетчика не должен сделать более одного оборота. 6. Установить минимальную нагрузку, при которой диск счетчика вращается непрерывно. Определить порог чувствительности счетчика. 7. Произвести поверку счетчика методом ваттметра и секундомера для нагрузок, указанных в табл. 9.4. Для этого установить напряжение U = 220 В и требуемую активную нагрузку (по ваттметру), отсчитать время t, в течение которого диск совершает N оборотов, рассчитать погрешности счетчика d, результаты измерений и вычислений записать в табл.9.4. (Число оборотов N указывает преподаватель.) Таблица 9.4
8. Сравнить результаты испытаний с требованиями ГОСТ 8.259 (табл. 9.1) и дать заключение об исправности счетчика. Содержание отчета 1. Паспортные данные счетчика, рассчитанные значения номинальной постоянной счетчика и номинальной мощности. 2. Схема электрической цепи для испытаний счетчика (рис. 9.3). 3. Таблицы вычислений и измерений, расчетные формулы. 4. Выводы о пригодности счетчика. Контрольные вопросы 1. Как устроен однофазный индукционный счетчик и каков его принцип действия? 2. Объяснить построение упрощенной векторной диаграммы счетчика. 3. При каком условии вращающий момент счетчика пропорционален активной мощности? 4. За счет чего создается тормозной момент? 5. Почему число оборотов диска пропорционально учитываемой активной энергии? 6. Что такое самоход счетчика, какова его причина и как он проверяется? 7. Что такое порог чувствительности? 8. Как определяется погрешность счетчика?
Лабораторная работа 1.10 ИЗМЕРЕНИЕ АКТИВНОЙ И РЕАКТИВНОЙ МОЩНОСТИ Цель работы: изучение методов измерения активной и реактивной мощности в трехфазных цепях. Общие сведения При симметричной нагрузке трехфазной цепи ( РА = РВ = РС = Р ф = U ф I ф cosj; QA = QB = QC = Q ф = U ф I ф sinj; P = 3 Р ф = 3 U ф I ф cosj = Q = 3 Q ф = 3 U ф I ф sinj = где j – угол сдвига фаз между фазным напряжением и фазным током. Полная мощность цепи
Приведенные формулы справедливы при любой схеме соединения трехфазной симметричной нагрузки (звездой или треугольником). Для измерения активной мощности любой фазы достаточно иметь один ваттметр и включить его на фазное напряжение и фазный ток (рис. 10.1). Показание ваттметра равно активной мощности одной фазы PW = P ф = U ф I Ф cosj. Активная мощность трехфазной цепи P = 3 PW. Рассмотренный метод измерения активной мощности симметричной цепи называют методом одного прибора.
Реактивную мощность фазы и всей симметричной цепи можно определить косвенным методом, дополнительно измеряя напряжение и ток фазы. Вычислив Однако реактивную мощность симметричной цепи можно измерить обычным ваттметром, включенным на «чужое напряжение». При этом параллельная обмотка ваттметра включается на «чужие фазы» по отношению к фазе, в которую включена последовательная (токовая) цепь прибора (рис. 10.2).
Как видно из векторной диаграммы (рис. 10.2б), показание ваттметра
Отсюда следует, что для определения реактивной мощности трехфазной симметричной цепи надо показание ваттметра увеличить в
В данном случае мгновенные мощности, учитываемые ваттметрами, p 1 = uAB iA; p 2 = uCB iC. Сумма этих мощностей равна мгновенной мощности трехфазной цепи p 1 + p 2 = uAB iA + uCB iC = uA iA + uB iB + uC iC = pA + pB + pC, так как uAB = uA – uB; uCB = uC – uB; iB = – (iA + iC). Переходя к средней или активной мощности, выраженной через действующие значения напряжений и токов, получим, что активная мощность, измеренная ваттметрами,
Таким образом, активная мощность, измеренная методом двух ваттметров, равна алгебраической сумме показаний ваттметров. На рис. 10.3б приведена векторная диаграмма для симметричной активно-индуктивной нагрузки. При этом угол между векторами Показания ваттметров P 1 = U л I л cos (j + 30°); P 2 = U л I л cos (j – 30°). Активная мощность всей цепи P = U л I л cos (j + 30°) + U л I л cos (j – 30°) = Показания ваттметров зависят от угла j = arctg R ф/ X ф (для параллельной схемы замещения). При активной нагрузке (j = 0) показания обоих ваттметров одинаковы
В случае j ¹ 0 показания ваттметров различны, причем если j = 60°, то При симметричной нагрузке методом двух ваттметров может быть рассчитана и реактивная мощность цепи. Рассмотрим разность показаний приборов: Р 2 – Р 1 = U л I л cos (j – 30°) – U л I л cos (j + 30°) = U л I л sinj. Как видно из выражения, для определения реактивной мощности цепи необходимо разность (Р 2 – Р 1) умножить на
По показаниям ваттметров можно выяснить характер нагрузки
Следует помнить, что это соотношение справедливо только при симметричной нагрузке. Предварительное задание к эксперименту Для электрической цепи, схема которой указана в табл. 10.1: 1. Рассчитать токи IA, IC, показания ваттметров, активную P и реактивную Q мощности симметричного приемника, соединенного звездой. Линейное напряжение сети U л = 220 В. Параметры параллельной схемы замещения активно-индуктивной нагрузки (R ф, Х ф) одной фазы приёмника заданы в табл. 10.1. 2. Результаты расчетов представить таблицей. 3. Построить векторную диаграмму напряжений и токов цепи. Таблица 10.1
Порядок выполнения эксперимента 1.Собрать электрическую цепь по схеме рис. 10.1. Измерить и записать в табл. 10.2 значения напряжения U л, тока I л, мощности PW для активной и активно-индуктивной симметричной нагрузки. По результатам измерений рассчитать мощности цепи P и Q. Таблица 10.2
2. Собрать электрическую цепь по схеме рис. 10.2. Измерить и записать в табл. 10.3 показания приборов для указанного в таблице характера симметричной нагрузки. Рассчитать реактивную мощность цепи Q. Таблица 10.3
3. Собрать электрическую цепь по схеме рис. 10.3. Измерить и записать в табл. 10.4 показания приборов для указанного в таблице характера нагрузки. Рассчитать активную Р и реактивную Q мощности цепи. Таблица 10.4
4. Сравнить результаты измерений с расчетными значениями, полученными в предварительном задании к эксперименту для соответствующей варианту цепи. Содержание отчета 1. Цель работы. 2. Схема соответствующей варианту трехфазной цепи и полный расчет предварительного задания к эксперименту. Таблица результатов расчета и векторная диаграмма. 3. Схемы электрических цепей для измерения мощности (две), исключая уже данную в предварительном задании. Векторные диаграммы напряжений и токов для этих цепей при смешанной нагрузке. 4. Таблицы измерений и вычислений (табл. 10.2, 10.3, 10.4). 5. Сравнительный анализ изученных методов измерения мощности. Контрольные вопросы 1. По каким формулам рассчитывают активную и реактивную мощности симметричной трехфазной цепи? 2. Какие методы используют для измерения активной мощности в трехфазных цепях? 3. Как можно определить реактивную мощность симметричной трехфазной цепи? 4. Когда применяется метод одного прибора, метод двух приборов, метод трех приборов? 5. Обосновать возможность измерения активной мощности трехфазной цепи методом двух ваттметров. 6. При каком условии и как можно определить реактивную мощность трехфазной цепи методом двух ваттметров? 7. В каком случае ваттметр PW 1 в схеме рис. 10.3 дает отрицательное показание? 8. В каком случае один ваттметр в схеме рис. 10.3 покажет нуль, а второй – мощность всей трехфазной цепи? 9. Каково устройство и принцип действия электродинамического ваттметра? Пояснить условные обозначения на шкалах ваттметров?
Лабораторная работа 1.11 исследование четырехполюсника Цель работы: 1) определение входных сопротивлений пассивного четырехполюсника (однофазного трансформатора) из опытов холостого хода и короткого замыкания; 2) определение коэффициентов пассивного четырехполюсника с помощью входных сопротивлений в режимах холостого хода и короткого замыкания; 3) расчет параметров Т– и П– образной схем замещения четырехполюсника. Общие сведения Четырехполюсником называют часть электрической цепи (или отдельное устройство), имеющую две пары зажимов (входные и выходные). В виде четырехполюсников удобно рассматривать однофазные трансформаторы, двухпроводные линии электропередачи, транзисторы, электронные усилители и т. д. Если четырехполюсник не содержит источников энергии, то он называется пассивным (рис. 11.1), а если содержит – активным (в прямоугольнике ставят букву А). Линейные пассивные четырехполюсники содержат только резистивные, индуктивные и емкостные элементы.
Ко входной паре зажимов (1–1¢) обычно подключается источник энергии, к выходной паре (2–2¢) - нагрузка Z н. Основная задача анализа четырехполюсника – аналитически связать между собой напряжения и токи на его входе U 1, I 1 и выходе U 2, I 2. Для линейных четырехполюсников эти величины связаны между собой системой двух линейных уравнений. В зависимости от того, какие величины приняты независимыми переменными, возможны шесть форм записи уравнений. В данной работе исследуется линейный пассивный четырехполюсник, для которого записываются уравнения в А– форме, при которой независимыми переменными являются U 2, I 2 (их называют основными уравнениями четырехполюсника):
Комплексные коэффициенты А, В, С, D зависят от схемы внутренних соединений четырехполюсника, от значений сопротивлений схемы и от частоты. Модули коэффициентов А и D – безразмерные величины, модуль коэффициента B измеряется в омах, С – в сименсах. Коэффициенты связаны соотношением А D – В С = 1. (11.2) Четырехполюсник называют симметричным, если при перемене местами источника питания и нагрузки токи в источнике питания и нагрузке не изменяются. В симметричном четырехполюснике А = D. Таким образом, для симметричного четырехполюсника достаточно определить три коэффициента, а четвертый можно найти из соотношения (11.2). На практике коэффициенты четырехполюсника А, В, С, D определяют с помощью его входных сопротивлений в режимах холостого хода и короткого замыкания, полученных расчетным или опытным путем. В режиме холостого хода, когда зажимы 2–2¢ разомкнуты, ток холостого тока I 2х=0. Тогда комплексное входное сопротивление четырехполюсника
В режиме короткого замыкания, когда зажимы 2–2¢ замкнуты накоротко, Z н=0, U 2к=0. Тогда входное сопротивление короткого замыкания четырехполюсника
Поменяем местами входные и выходные зажимы четырехполюсника, подключив источник к зажимам 2–2¢ (Рис. 11.2)
Уравнения четырехполюсника при питании его со стороны зажимов 2–2¢ и подключении нагрузки к зажимам 1–1¢:
Проведем опыт холостого хода со стороны зажимов 1–1¢, когда I 2х=0. Из уравнений (11.5) получаем входное сопротивление со стороны зажимов 2–2¢
Трех опытов достаточно для определения коэффициентов А, В, С, D, так как используем уравнение (11.2). Решая совместно четыре уравнения (11.3), (11.4), (11.6) и (11.2), получим выражение комплексного коэффициента А:
Затем коэффициенты С, D, В определяем соответственно по уравнениям (11.3), (11.6) и (11.4). Для симметричного четырехполюсника их можно определить из опытов холостого хода и короткого замыкания только со стороны входных зажимов
Любой четырехполюсник может быть представлен двумя эквивалентными схемами замещения: Т– образной (рис. 11.3 а) – схема звезды и П– образной (рис. 11.3 б) – схема треугольника:
Три сопротивления Т– или П– образной схем замещения должны быть рассчитаны из условия, чтобы схема замещения обладала такими же коэффициентами А, В, С, D, какими обладает заменяемый ею четырехполюсник. Выразим напряжение U 1 и ток I 1 в Т– образной схеме через U 2 и ток I 2:
|

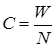 , численно равный энергии, приходящейся на один оборот диска, называют действительной постоянной счетчика.
, численно равный энергии, приходящейся на один оборот диска, называют действительной постоянной счетчика. .
.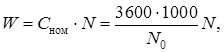
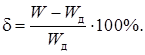

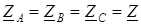 ) активная и реактивная мощность всех фаз одинакова и для определения мощности цепи достаточно измерить мощность одной фазы, затем результат утроить:
) активная и реактивная мощность всех фаз одинакова и для определения мощности цепи достаточно измерить мощность одной фазы, затем результат утроить: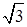 U л I л cosj;
U л I л cosj;
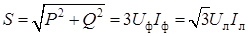 .
.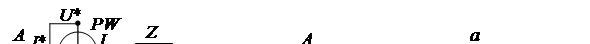
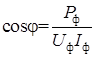 , получим Q ф = U ф I ф sinj, Q = 3 Q ф.
, получим Q ф = U ф I ф sinj, Q = 3 Q ф.
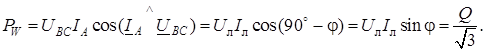
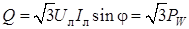
 Основным методом измерения активной мощности в трехпроводных трехфазных цепях при любой асимметрии цепи является метод двух ваттметров (рис. 10.3).
Основным методом измерения активной мощности в трехпроводных трехфазных цепях при любой асимметрии цепи является метод двух ваттметров (рис. 10.3).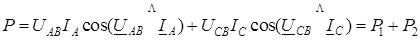 .
.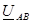 и
и 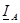 равен (j + 30°), а угол между векторами
равен (j + 30°), а угол между векторами 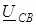 и
и 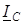 равен (j – 30°).
равен (j – 30°).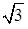 U л I л cos j.
U л I л cos j.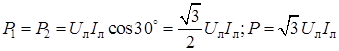 .
.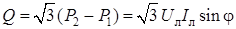 .
.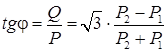 .
.
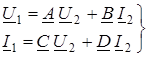 (11.1)
(11.1)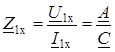 . (11.3)
. (11.3)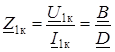 . (11.4)
. (11.4)
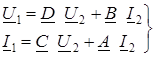 . (11.5)
. (11.5)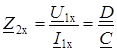 . (11.6)
. (11.6)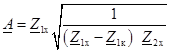 . (11.7)
. (11.7)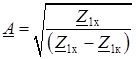 ;
; 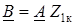 ;
; 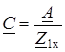 ;
; 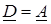 . (11.8)
. (11.8)
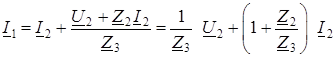 ,
,


