Решение. В неоклассической модели роста была использована производственная функция вида Y=AF(K, L)
В неоклассической модели роста была использована производственная функция вида Y=AF(K, L). Объем производства Y зависит от вклада факторов — труда L и капитала К, а также от технологии. Производственная функция имеет постоянную отдачу от масштаба, т.е. увеличение всех факторов в определенной степени приводит к росту выпуска в той же степени (если факторы увеличились вдвое, то выпуск возрастет также в 2 раза). Изменение выпуска можно представить как Разделим это выражение на Y = A-F(K, L) и получим:
Второе и третье слагаемые правой части уравнения умножим и разделим на К и L:
В скобках мы получим доли капитала и труда в общем объеме выпуска. При условии постоянной отдачи от масштаба сумма этих долей равна
248 Макроэкономика единице (по теореме Эйлера), тогда
— доля труда в доходе; А — общая производительность факторов, мера уровня технологического прогресса, измеряемая обычно по остаточному принципу ("остаток Солоу")1. В представленной функции
проверить математически, проведя с этой функцией все указанные выше операции. Тогда растет с темпом 3,9% в год. 2. Производственная функция задана уравнением
|

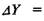
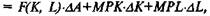 где МРК и MPL — предельные производительности соответствующих факторов.
где МРК и MPL — предельные производительности соответствующих факторов.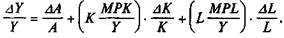
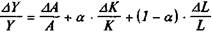 , где а — доля капитала, а (1-α)
, где а — доля капитала, а (1-α) показатели степе-
показатели степе- ни представляют собой одновременно и долю факторов в доходе, то есть, что можно
ни представляют собой одновременно и долю факторов в доходе, то есть, что можно , т.е. выпуск
, т.е. выпуск Норма сбережения s равна 0,2, норма выбытия d — 5%, темп роста населения я составляет 2% в год, темп трудосберегающего технологического прогресса g равен 3%. Каким будет запас капитала и объем выпуска в расчете на одного занятого в устойчивом состоянии? Соответствует ли устойчивая фондовооруженность уровню, при котором достигается максимальный объем потребления ("золотому правилу")? Какой должна быть норма сбережения в соответствии с "золотым правилом"?
Норма сбережения s равна 0,2, норма выбытия d — 5%, темп роста населения я составляет 2% в год, темп трудосберегающего технологического прогресса g равен 3%. Каким будет запас капитала и объем выпуска в расчете на одного занятого в устойчивом состоянии? Соответствует ли устойчивая фондовооруженность уровню, при котором достигается максимальный объем потребления ("золотому правилу")? Какой должна быть норма сбережения в соответствии с "золотым правилом"?


