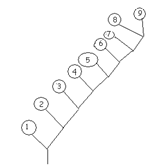
В саду ветвящихся дорожек

1. В Саду каждая дорожка либо разветвляется на две, либо заканчивается клумбой. От входа ведет одна дорожка. Может ли в саду быть 9 клумб? (Если может – нарисуйте картинку, если нет – объясните почему).

Да, может.

2. На этой клумбе все цветы, кроме двух – маки, все цветы, кроме двух - тюльпаны, и все цветы, кроме двух – гладиолусы. Сколько цветов на этой клумбе?

Поскольку все цветы, кроме двух – маки, гладиолусов и тюльпанов не более двух. Пусть тюльпанов 2, тогда гладиолусов – 0, тогда маков тоже ноль, так как все, кроме двух тюльпанов, - гладиолусы. Но тогда тюльпаны – все, а надо чтобы было 2 не тюльпана. Аналогично с двумя гладиолусами… Значит есть один тюльпан и один гладиолус. Все кроме двух – тюльпаны, один из них – гладиолус, значит второй – мак. Значит мак – тоже один.

Итак, на клумбе по одному цветку каждого вида.

3. Между клумбами есть подземные туннели. Две клумбы соединены туннелем тогда и только тогда, когда сумма их номеров делится на три без остатка. Может ли крот, который умеет ползать только по туннелям, попасть с клумбы №3 к клумбе №5, возможно, через другие клумбы?

Клумба номер 3 соединена только с клумбами №6 и №9. Клумба №6 – только с №3 и №9. А клумба №9 – с №3 и №6. Значит никуда кроме клумб №3,6,9 крот добраться не может.

4. Самый Мудрый Крот решил усовершенствовать сеть подземных туннелей. Какое минимальное количество туннелей надо прорыть, чтобы из каждой клумбы можно было попасть в каждую, возможно проползая через другие?

Имелось в виду, что мы все в том же саду, где клумб 9. Прорыть надо 8 туннелей. Чтобы доказать, что восьми достаточно, важно привести схему (или описать ее): соединяем клумбы 1-2-3-4-5-6-7-8-9.

Строгое доказательство того, что меньшим числом не обойтись, достаточно сложное, и его от учеников ожидать не нужно. Однако надо понимать, что, в принципе, в таких задачах надо доказывать минимальность.

5. Когда кроты прорыли все туннели, Секретная Служба решила уничтожить схему, которая была нарисована на листе бумаги. Поэтому вначале они порвали схему на три части, потом какой-то из ее кусков еще на три части и так далее. Шпион нашел 12 кусков схемы. Все ли куски нашел Шпион?

В начале было 3 части. Если разорвать одну из частей на 3 части, то количество кусков увеличится на 2 (один кусок порвали и три добавили). Значит число кусков будет 3, 5, 7…, то есть нечетным. А крот нашел 12 кусков – четное число, значит не все куски.