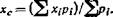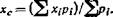
Учитывая, что У х;р; = М (X) и 2 Р/= 1 > получим М (Х) — хс.
Итак, математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы — их вероятностям.
Замечание 2. Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (XVI — XVII вв.), когда область ее применения ограничивалась азарта Ымн играми. Игрока интересовало среднее значение ожидаемого выигрыша, или, иными словами, математическое ожидание выигрыша.