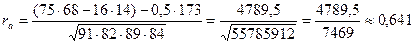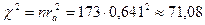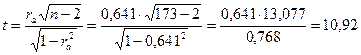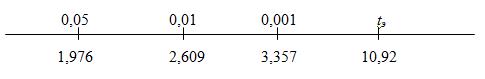Решение. Взаимосвязь переменных измеренных в шкале наименований, группируемых в таблицу 2х2 можно измерить с помощью коэффициента ассоциации
Взаимосвязь переменных измеренных в шкале наименований, группируемых в таблицу 2х2 можно измерить с помощью коэффициента ассоциации, предложенного К. Пирсоном (1901 г.). Коэффициент ассоциации может быть использован в том случае если n<30 и fт <5. Рассчитывается по формуле:
где a, b, c, d – количество наблюдений в ячейках таблицы сопряженности 2х2. Коэффициент ассоциации изменяется от -1 до +1. Значимость коэффициента ассоциации оценивают по величине критерия χ2-Пирсона при df =1. Основную гипотезу отвергают, если Значимость коэффициента ассоциации можно оценить и с помощью t-критерия Стьюдента, основную гипотезу отвергают, если
Принято вносить поправку Йетса в формулу Ограничения метода: используется только для таблиц сопряженности 2х2 1 шаг. Формулируем статистические гипотезы: Н0: показатели самооценки и притязаний студентов не взаимосвязаны Н1: показатели самооценки и притязаний студентов взаимосвязаны (ненаправленная гипотеза); чем выше уровень самооценки, тем выше уровень притязаний (направленная гипотеза) или чем выше уровень притязаний, тем выше уровень самооценки. 2 шаг. Строим таблицу сопряженности.
3 шаг. Проверяем ограничения критерия: таблица сопряженности 2х2, следовательно, критерий применим. 4 шаг. Вычисляем эмпирическое значение
Эмпирическая частота каждой ячейки и подставляется в формулу:
Рассчитаем
5 шаг. Оценим значимость коэффициента ассоциации по величине критерия χ2-Пирсона при df =1. Теперь построим ось значимости:
Следовательно подтверждается Н1 при р<0,001. Оценим значимость коэффициента ассоциации по величине t-критерия Стьюдента при df =173-2=171. Теперь построим ось значимости:
Следовательно подтверждается Н1 при р<0,001. 6 шаг. Принимаем статистическое решение. По оси значимости видим, что р-уровень р<0,001, и в этом случае мы можем принять подтверждение ненаправленной гипотезы Н1: показатели самооценки и притязаний взаимосвязаны (на 99% уровне точности). При проверке направленной гипотезы р-уровень значимости будет р\2=0,0005. Содержательный вывод: чем выше самооценка, тем выше уровень притязаний.
|


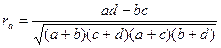 ,
,
 при df = n – 2
при df = n – 2
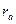 коэффициент ассоциации Пирсона. Каждая ячейка таблицы сопряженности обозначается буквенным символом:
коэффициент ассоциации Пирсона. Каждая ячейка таблицы сопряженности обозначается буквенным символом: