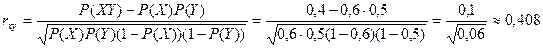Решение. Где P(XY) – число совпадений положительных знаков в вариационном ряду, отнесенное к общему числу случаев
Где P(XY) – число совпадений положительных знаков в вариационном ряду, отнесенное к общему числу случаев, P(X) и P(Y) – количество положительных знаков отдельно по каждому признаку, отнесенное к общему числу случаев. Коэффициент корреляции знаков может принимать значение от 0 до 1. Оценка достоверности коэффициента корреляции знаков отсутствует. Можно ориентироваться по классификации корреляционных связей по их силе (по Э.В. Ивантер, А.В. Коросову, 1992) [Сидоренко, с. 203 – 204]:
Ограничения метода: нет 1 шаг. Формулируем статистические гипотезы: Н0: показатели увлеченности знаниями и склонность учащихся к математике не взаимосвязаны Н1: показатели увлеченности знаниями и склонность учащихся к математике взаимосвязаны 2 шаг. Вычисляем эмпирическое значение коэффициента корреляции знаков:
P(XY)=4/10=0,4 P(X)=6/10=0,6 P(Y)=5/10=0,5
3 шаг. Принимаем статистическое решение. Используя классификацию корреляционных связей по их силе, делаем вывод о значимости взаимосвязи переменных. Наблюдается умеренная взаимосвязь между увлеченностью знаниями и склонностью учащихся к математике. Содержательный вывод: учащиеся, увлеченные знаниями, проявляют склонность к математике. Это может быть объяснено тем, что увлеченность знаниями определяется в первую очередь высоким познавательным мотивом, что в свою очередь определяет склонность к изучению основ наук. 2.24. Выясняли зависимость между упрямством детей (Х) и строгостью требований родителей (У). Под наблюдением находилось 15 учащихся и их родителей из разных семей.
|

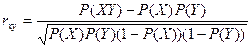 ,
,