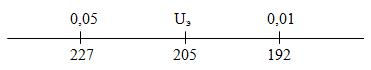Решение. n1 – количество испытуемых в выборке 1

,

n₁ – количество испытуемых в выборке 1

n₂ – количество испытуемых в выборке 2

Т_х – большая из двух ранговых сумм

n_x – количество испытуемых в группе с большей суммой рангов

Применение критерия U-Манна-Уитни отличается для одинаковых и различных по численности выборок:

1. n₁=n₂

В этом случае эмпирическая величина U рассчитывается только для большей ранговой суммы.

2. n₁ ≠n₂

В этом случае необходимо подсчитать величину U и для второй ранговой суммы, подставляя в формулу соответствующее ей n_x. Из двух полученных величин выбирается меньшая. Для определения критического значения U необходимо определить n₁ и n₂. Меньшее n принимается за n₁, большее n принимается за n₂.

Для решения данной задачи необходимо применить критерий U Манна-Уитни трижды: сравнение представлений о профессии студентов 1 и 2 курсов, 1 курса и преподавателей, 2 курса и преподавателей.

Сравним представление о профессии студентов 1 и 2 курсов.

1 шаг. Формулируем статистические гипотезы:

Н₀: представления о профессии «Повар-кондитер» студентов 1 и 2 курсов не отличаются

Н₁: представления о профессии «Повар-кондитер» студентов 1 и 2 курсов отличаются (ненаправленная гипотеза)

2 шаг.

Проверка ограничений

1. В каждой выборке должно быть не менее 3 наблюдений n₁, n₂=25

2. В каждой выборке должно быть не более 60 наблюдений, n₁, n₂=25

Ограничения снимаются

3 шаг. Введем условные обозначения: студентов 1 курса обозначим 1, 2 курса – 2.

Так как данные представлены в интервальной шкале их необходимо перевести в ранговую шкалу. Для этого построим упорядоченный ряд из всех значений, полученных данных. Значения проранжируем с учетом связанных рангов по принципу меньшему значению – меньший ранг.

Представления о профессии	Предварительный Ранг	Окончательный ранг	Группа	Ранги 1 группы	Ранги 2 группы
3,17
3,33
3,47
3,5
3,53
3,57
3,67
3,8
		9,5		9,5
		9,5		9,5
4,03
4,1
4,17
4,2		15,5		15,5
4,2		15,5			15,5
4,2		15,5			15,5
4,2		15,5			15,5
4,23		18,5		18,5
4,23		18,5			18,5
4,27		20,5			20,5
4,27		20,5		20,5
4,3		22,5		22,5
4,3		22,5			22,5
4,33
4,33
4,33
4,37
4,37
4,37
4,4		30,5			30,5
4,4		30,5			30,5
4,43
4,47
4,5
4,5
4,5
4,5
4,5
4,53		39,5			39,5
4,53		39,5			39,5
4,6		42,5			42,5
4,6		42,5		42,5
4,6		42,5		42,5
4,6		42,5			42,5
4,63		45,5			45,5
4,63		45,5			45,5
4,67
4,7
4,7
4,7
ΣR

4 шаг. Проверка правильности проведенного ранжирования:

ΣR=1275

Суммы совпадают, следовательно, ранжирование проведено правильно.

5 шаг. Необходимо сосчитать ранговые суммы по каждой выборке в отдельности.

Т₁=530

Т₂=745

6 шаг. Вычисляем эмпирическое значение U-Манна-Уитни

7 шаг. Определяем критическое значение U-Манна-Уитни для n₁ =25 и n₂ =25 таблица критических значений см. прил. …. Теперь построим ось значимости.

8 шаг. Принимаем статистическое решение. По оси значимости видим, что р-уровень р<0,05, и в этом случае мы можем принять подтверждение гипотезы Н₁: представления о профессии «Повар-кондитер» студентов 1 и 2 курсов отличаются.

 

Используя данный пример, рассчитайте критерий U при условии, когда выборки различны по объему, т.е. сравним представления о профессии студентов 1 курса и преподавателей.