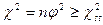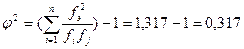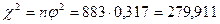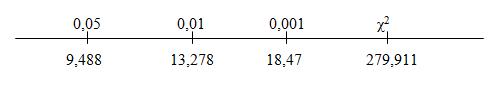Решение. fi – сумма частот по строкам, fj – сумма частот по столбцам
fi – сумма частот по строкам, fj – сумма частот по столбцам Данный критерий с поправкой А.А. Чупрова
Значимость коэффициента взаимной сопряженности оценивают по величине критерия χ2-Пирсона при df =(nx,-1)(ny -1). Основную гипотезу отвергают, если Ограничения метода:
1 шаг. Формулируем статистические гипотезы: Н0: показатели самооценки и выбор учащимися задач разной сложности не взаимосвязаны Н1: показатели самооценки и выбор учащимися задач разной сложности взаимосвязаны. 2 шаг. Строим таблицу сопряженности.
3 шаг. Проверяем ограничения критерия: fэ >5, N>50,следовательно, критерий применим. 4 шаг. Вычисляем эмпирическое значение коэффициента взаимной сопряженности с поправкой А.А. Чупрова. Сначала рассчитаем значение
Подставим все значения в формулу коэффициента взаимной сопряженности с поправкой А.А. Чупрова:
5 шаг. Оценим значимость коэффициента ассоциации по величине критерия χ2-Пирсона при df =(3-1)(3-1)=4 6 шаг. Построим ось значимости:
7 шаг. Принимаем статистическое решение. По оси значимости видим, что р-уровень р<0,001, и в этом случае мы можем принять подтверждение гипотезы Н1: показатели самооценки и выбор учащимися задач разной сложности взаимосвязаны (на 99% уровне точности). Содержательный вывод: учащиеся с низкой самооценкой чаще выбирают простые задачи, которые они с большей вероятностью могут решить. Учащиеся со средней и высокой самооценкой выбирают задачи средней степени сложности, вероятность решения которых уже не так однозначна. Задачи повышенной сложности чаще выбирают ученики с высокой самооценкой, чем с низкой и средней. 2.23. Оценивали взаимосвязь психического выгорания медицинских работников и уровень стрессоустойчивости. Были получены следующие данные:
Оцените, взаимосвязаны ли переменные.
|

 , где
, где 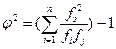
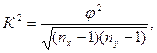 где К2 – коэффициент взаимной сопряженности Чупрова, nx, ny – численность групп по строкам и столбцам таблицы сопряженности.
где К2 – коэффициент взаимной сопряженности Чупрова, nx, ny – численность групп по строкам и столбцам таблицы сопряженности.