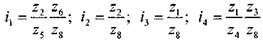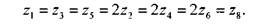КИНЕМАТИЧЕСКИЙ РАСЧЕТ КОРОБОК СКОРОСТЕЙ
Для кинематических расчетов коробок скоростей в станкостроении применяются два метода: аналитический и графоаналитический. Оба метода позволяют находить величины передаточных отношений передач, входящих в коробку скоростей. Однако, как правило, используют только графоаналитический метод. Достоинством его является то, что он позволяет более быстро находить возможные варианты решения, дает большую наглядность (что облегчает сравнение вариантов). При графоаналитическом методе последовательно строят структурную сетку и график (картину) частоты вращения. Структурная сетка дает ясное представление о структуре привода станка. По структурной сетке легко прослеживаются связи между передаточными отношениями групповых передач (групповой передачей называется совокупность передач между двумя последовательными валами коробки скоростей); однако сетка не дает конкретных значений этих величин. Она наглядно характеризует ряд структур приводов в общей форме. Структурная сетка содержит следующие данные о приводе: число групп передач, число передач в каждой группе, относительный порядок конструктивного расположения групп вдоль цепи передач, порядок кинематического включения групп (т.е. их характеристики и связь между передаточными отношениями), диапазон регулирования групповых передач и всего привода, число ступеней скорости вращения ведущего и ведомого валов групповой передачи. График (картина) частоты вращения позволяет определить конкретные величины передаточных отношений всех передач привода и частоты вращения всех его валов. Он строится в соответствии с кинематической схемой привода. При разработке кинематической схемы коробки скоростей станка с вращательным главным движением должны быть известны число ступеней частоты вращения шпинделя z, знаменатель геометрического ряда ф, частоты вращения шпинделя от п\ до nz и частота вращения электродвигателя пэд.
Число ступеней частоты вращения шпинделя z при настройке последовательно включенными групповыми передачами (в многоваловых коробках) равно произведению числа передач в каждой группе, т.е. z=papbPc---Pk-Например, для привода, показанного на рисунке 9, z= рарьрс=3-2-2=12. При заданном (или выбранном) числе ступеней ряда частоты враще- ния шпинделя z число групп передач, число передач в каждой группе и порядок расположения групп можно выбирать различными. Этот выбор в основном и определяет кинематику и конструкцию коробки скоростей. Для наиболее часто применяемых значений z могут быть использованы следующие конструктивные варианты:
В станках с изменением частоты вращения шпинделя по геометрическому ряду передаточные отношения передач в группах образуют геометрический ряд с знаменателем фх, где х - целое число, которое называется характеристикой группы. Характеристика группы равна числу ступеней скорости совокупности групповых передач, кинематически предшествующих данной группе. Общее уравнение настройки групповых передач имеет следующий вид: Для последовательного Для конструктивного варианта привода, показанного на рисунке 9, и принятого порядка переключений скоростей можно записать структурную формулу 7=3(1)2(6)2(3). В формуле цифрами в скобках обозначены характеристики групп. Основной и различными поп номеру переборными группами может быть любая другая группа передач в приводе, поэтому наряду с конструктивными вариантами привода возможны также различные его кинематические варианты.
отсюда наибольший диапазон регулирования групповой передачи будет
где xmax - наибольший показатель для последней переборной группы; р - число передач в этой группе. Для графического изображения частот вращения шпинделя станка обычно используют логарифмическую шкалу чисел. С этой целью геометрический ряд частот вращения
Таким образом, если откладывать на прямой линии последовательные значения логарифмов частот вращения пь п2, п3,..., nz, то интервалы между ними будут постоянны и равны lg ф.
Для принятого конструктивного варианта привода возможны два варианта структурной формулы: z=6=3(l)-2(3) и z=6=3(2)-2(l). В первом случае основной группой будет первая в конструктивном отношении группа передач, а первой переборной - вторая группа передач; для второго случая - наоборот. На рисунке 10, б, в показаны структурные сетки для приведенных формул структуры привода. Они построены следующим образом. На равном расстоянии друг от друга проводят вертикальные линии, число которых должно быть на единицу больше, чем число групповых передач. Также проводят ряд горизонтальных параллельных прямых с интервалом, равным lg ф (число горизонтальных прямых равно числу ступеней z частоты вращения шпинделя). На середине первой слева вертикальной линии наносят точку О, из которой симметрично в соответствии с числом передач в группах по заданной структурной формуле проводят лучи, соединяющие точки на вертикальных линиях. Расстояния между соседними лучами должны быть равны X; lg ф, где X; — характеристика соответствующей группы. Оптимальный вариант структурной сетки выбирают следующих выражений. Выше отмечалось, что независимо от порядка переключений групповых передач диапазон регулирования последней переборной группы является наибольшим. Поэтому следует определить диапазоны регулирования последних переборных групп для всех вариантов структурных сеток (при выбранном значении ф) и исключить из дальнейшего рассмотрения варианты, не удовлетворяющие условию
Для варианта, показанного на рисунке 10, б, хтах=3, а для варианта, показанного на рисунке 10, в, хтах=2. Вариант б подходит для всех значений ф, так как 2(2" 1)3=8; вариант в удовлетворяет всем значениям ф за исключением ф=1,78 и ф=2 поскольку 1,78(3"1>2>8 и 2(3'1}'2>8. На рисунке 10, г, д показаны построенные для обоих вариантов структурных сеток графики частоты вращения при 0=1,26, ni=160 об/мин, п6=500 об/мин и п=1000 об/мин. Графики частоты вращения строят в следующей последовательности: на равном расстоянии друг от друга проводят вертикальные линии, число которых равно числу валов коробки; на равном расстоянии друг от друга с интервалами lg ф проводят горизонтальные линии, которым присваивают (снизу вверх) порядковые частоты вращения, начиная с п\. Луч, проведенный между вертикальными линиями, обозначает передачу между двумя валами с передаточным отношением 1=фт, где т - число интервалов lg ф, перекрытых лучом. При горизонтальном положении луча 1=1, при луче, направленном вверх, i>l, а вниз i<l. Для разбираемого примера (ф=1,26) с учетом особенностей отдельных передач и значений предельных передаточных отношений строим (для каждого варианта)
По этим формулам находятся числа зубьев колес группы по заданной ^]z. Передаточные отношения ib 12и т.д. определяют из графика частоты вращения.
Коробки подач предназначены для получения требуемых величин подач и сил подачи при обработке на станке различных деталей. Коробка подач в большинстве случаев заимствует движение от шпинделя станка или приводится в движение от отдельного электродвигателя. Значения подач должны обеспечивать требуемую шероховатость поверхности, а также высокую стойкость инструмента и производительность станка. Подачи в общем случае должны располагаться в геометрической прогрессии. Изменение величины подачи можно производить различными способами: с помощью механизмов с зубчатыми передачами и без применения зубчатых передач (например, электрическим и гидравлическим путем, храповым и кулачково-рычажным механизмами и т.д.). Коробки подач с зубчатыми передачами бывают: а) со сменными зубчатыми колесами, с постоянным расстоянием между осями валов; б) с передвижными блоками зубчатых колес; в) со встречными ступенчатыми конусами колес и вытяжными шпонками; г) нортоновские; д) в форме гитар сменных зубчатых колес; е) с механизмами типа Меандра. Для получения большого количества величин подач коробки часто конструируют, используя сразу несколько из перечисленных механизмов. Коробки подач со сменными зубчатыми колесами (с постоянным расстоянием между осями валов) находят применение в станках для крупносерийного производства при редкой настройке. В частности, такие коробки встречаются в автоматах, полуавтоматах, операционных и специальных станках. Конструкции коробок подач, состоящих из одних лишь сменных зубчатых колес, очень просты и не отличаются от обычных коробок скоростей. Коробки подач с передвижными блоками зубчатых колес широко применяют в универсальных станках. Они позволяют передавать большие крутящие моменты и работать с большими скоростями. К недостатку коробок подач этого типа относится невозможность использования в них косозубых колес. По конструкции коробки подач с передвижными зубчатыми колесами аналогичны соответствующим коробкам скоростей. Коробка подач со встречными ступенчатыми контурами колес и вытяжной шпонкой на четыре различных передаточных отношения (вообще число передач в таких коробках может достигать 8-10 в одной группе) показана на рисунке 11, а, передача движения в ней осуществляется через пару зубчатых колес
группы передач коробки подач. В механизме с вытяжной шпонкой (рисунок 11, б) на верхнем ведущем валу жестко закреплены на шпонке зубчатые колеса zb z3, z5 и z7, которые находятся в постоянном зацеплении соответственно с зубчатыми колесами z2, z4, z6 и z8. Одно из зубчатых колес, расположенных на ведомом валу, посредством вытяжной шпонки может быть жестко связано с валом, и тогда вращение валу передается через это колесо. При этом остальные зубчатые колеса вращаются вхолостую. Во избежание одновременного включения двух ведомых зубчатых колес механизм имеет специальные разделительные кольца 1. Недостатком этого механизма является то, что зубчатые колеса ведомого вала независимо от того, передают они крутящий момент или нет, постоянно вращаются, что ускоряет их износ и требует дополнительной затраты мощности. К недостаткам относятся также возможность перекоса вытяжной шпонки, малая жесткость шпоночного валика, ослабленного продольным пазом, вращение колес с чрезмерно большой скоростью, если шпоночный валик работает как ведущий и др. Коробки подач с вытяжными шпонками применяют в небольших, а иногда и в средних по размеру сверлильных и токарно-револьверных станках. Механизм Нортона показан на рисунке 11, в. Этот механизм позволяет получить арифметический ряд подач, необходимый при нарезании стандартных резьб; поэтому его широко применяют в коробках подач токарно-винторезных станков. Его достоинствами являются малые размеры вдоль оси и возможность свободного выбора передаточных отношений независимо от межцентрового расстояния. Он позволяет получить при небольших размерах большое количество передаточных отношений, необходимых для нарезания разных резьб с различным шагом. На ведущий вал I свободно надет рычаг 1, с помощью которого зубчатое колесо zb находящееся постоянно в зацеплении с колесом z2, перемещается вдоль вала. Накидывая колесо z2 на одно из колес ведомого зубчатого конуса, получают соответствующее передаточное отношение. В нашем примере механизм типа Нортона имеет 4 передаточных отношения:
Существуют нортоновские передачи, у которых число передаточных отношений достигает 10-12 при приемлемых осевых размерах коробки. Ведущим звеном может быть и зубчатый конус, т.е. передача является обратимой. Коробки подач в форме гитар сменных зубчатых колес (рисунок 11, г). Гитарой называется устройство, обеспечивающее надлежащее сцепление сменных зубчатых колес. Гитары сменных колес дают возможность настраивать подачу с любой степенью точности. Они позволяют применять передаточные отношения до imin=1/8. Гитары бывают двухпарные и трехпарные. В основном в станках встречаются двухпарные гитары, лишь в редких случаях, когда необходимы особенно малые передаточные отношения, используют трехпарную гитару. Каждую гитару снабжают определенным комплектом сменных зубчатых колес. Например, для токарно-винторезных станков рекомендуется комплект сменных зубчатых колес из z=20, 24, 25, 28, 30, 32, 36, 40, 44, 45, 48, 50, 55, 60, 65, 68, 70, 71, 75, 76, 80, 85, 90, 95, 100, 110, ИЗ, 120, 127. На рисунке 20, г показана схема двухпарной гитары. Расстояние А между ведущим валом 1 (колеса а) и ведомым 2 (колеса d) является неизменным. На ведомом валу свободно посажен приклон гитары 3. В приклоне имеются радиальный и дуговой пазы. В радиальном пазу крепят ось 4 колес b и с. Перемещая ось вдоль паза, можно менять расстояние В между колесами сие. Вследствие наличия дугового паза в приклоне имеется возможность изменять расстояние С между колесами а и Ь, поворачивая приклон на валу 2. В требуемом положении приклон закрепляют болтом 5. Механизм Меандра (рисунок 11, д) состоит из трехпарных зубчатых колес. Колеса z\ и z2 жестко закреплены на ведущем валу, a z3, z4, z5 и z6 свободно вращаются на промежуточном валу. Зубчатое колесо z7 является накидным и всегда находится в зацеплении с передвижным колесом z8. переключение производится рычагом 1. показанный механизм дает 4 передаточных отношения:
Подобные механизмы могут быть и с большим количеством передаточных отношений. Числа зубьев колес механизма подбирают так, чтобы
|

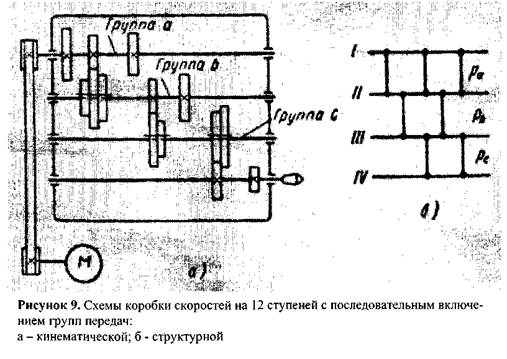
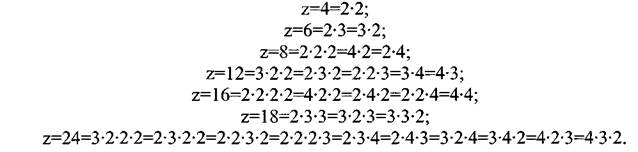
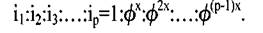 получения всех частот вращения шпинделя сначала переключают передачи одной группы, затем другой и т.д. Если в коробке скоростей, показанной на рисунке 9, использовать с этой целью передачи группы а, затем группы сив последнюю очередь группы Ь, то соответственно этому порядку переключений группа а будет основной, группа с - первой переборной, группа b -второй переборной. Коробка скоростей может иметь и большее число переборных групп. Для основной группы передач характеристика хо=1; для первой переборной группы xi=pi; для второй переборной группы x2-pip2 и т.д., где piH p2 - соответственно числа передач основной и первой переборной групп.
получения всех частот вращения шпинделя сначала переключают передачи одной группы, затем другой и т.д. Если в коробке скоростей, показанной на рисунке 9, использовать с этой целью передачи группы а, затем группы сив последнюю очередь группы Ь, то соответственно этому порядку переключений группа а будет основной, группа с - первой переборной, группа b -второй переборной. Коробка скоростей может иметь и большее число переборных групп. Для основной группы передач характеристика хо=1; для первой переборной группы xi=pi; для второй переборной группы x2-pip2 и т.д., где piH p2 - соответственно числа передач основной и первой переборной групп. Во избежание чрезмерно больших диаметров зубчатых колес в коробках скоростей, а также в целях нормальной их работы практикой установлены следующие предельные передаточные отношения между валами при прямозубом зацеплении:
Во избежание чрезмерно больших диаметров зубчатых колес в коробках скоростей, а также в целях нормальной их работы практикой установлены следующие предельные передаточные отношения между валами при прямозубом зацеплении: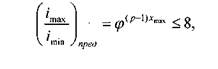
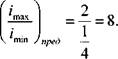
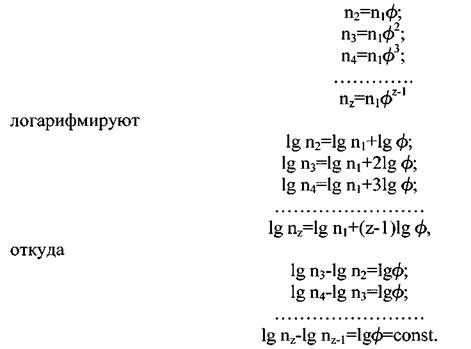
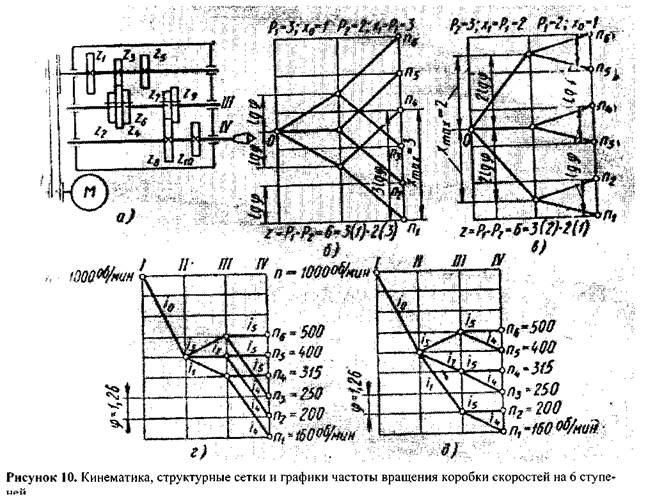 Рассмотрим построение структурной сетки и графика частоты вращения для коробки скоростей, кинематическая схема которой показана на рисунке 10, а.
Рассмотрим построение структурной сетки и графика частоты вращения для коробки скоростей, кинематическая схема которой показана на рисунке 10, а.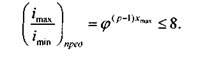
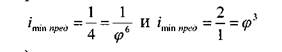 сначала цепь передач для снижения частоты вращения от п=1000 до ni=160 об/мин. Наиболее целесообразно при этом разбить общее передаточное отношение этой цепи так, чтобы сохранить более высокими частоты вращения промежуточных валов. В этом случае размеры коробки уменьшаются. Дальнейшее построение ведем, используя принятые варианты структурных сеток. Построенный график частоты вращения позволяет определить передаточное отношение всех передач коробки.
сначала цепь передач для снижения частоты вращения от п=1000 до ni=160 об/мин. Наиболее целесообразно при этом разбить общее передаточное отношение этой цепи так, чтобы сохранить более высокими частоты вращения промежуточных валов. В этом случае размеры коробки уменьшаются. Дальнейшее построение ведем, используя принятые варианты структурных сеток. Построенный график частоты вращения позволяет определить передаточное отношение всех передач коробки.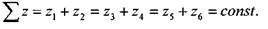 По найденным передаточным отношениям определяют числа зубьев зубчатых колес. Следует иметь в виду, что в станкостроении межосевые расстояния, суммы чисел зубьев сопряженных колес, числа зубьев червячных колес и модули нормализованы. При постоянном расстоянии между осями ведущего и ведомого валов и одинаковом модуле колес группы передач сумма чисел зубьев каждой пары зубчатых колес является постоянной величиной, т.е.
По найденным передаточным отношениям определяют числа зубьев зубчатых колес. Следует иметь в виду, что в станкостроении межосевые расстояния, суммы чисел зубьев сопряженных колес, числа зубьев червячных колес и модули нормализованы. При постоянном расстоянии между осями ведущего и ведомого валов и одинаковом модуле колес группы передач сумма чисел зубьев каждой пары зубчатых колес является постоянной величиной, т.е.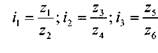 Передаточные отношения пар зубчатых колес, находящихся в зацеплении:
Передаточные отношения пар зубчатых колес, находящихся в зацеплении: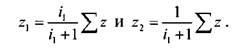 и т.д. Из уравнений
и т.д. Из уравнений 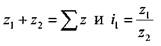 следует
следует
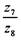 . Механизмы с вытяжными шпонками обычно используют в качестве основной
. Механизмы с вытяжными шпонками обычно используют в качестве основной