Точка в квадрантах і октантах простору
Рис. 1.15 Площини П1, П2, П3ділять простір на вісім у геометричному відношенні одинакових частин – октантів (рис. 1.16).
Рис. 1.16
Знаки координат точок за октантами подано в таблиці:
На рис 1.17 наведено комплексне креслення в системі площин (П1П2П3) точок А(3; 4; 2) і В (2; 3; -2), С (-1; 0; 3). Одиницю виміру позначено штрихом на координатних осях. Точка А знаходиться в першому октанті, точка В – у четвертому октанті, точка С належить площині П2. Слід відмітити, що точка С одночасно належить п’ятому та шостому октантам.
Рис. 1.17 Рис. 1.18 На рис. 1.18 наведено комплексне креслення в системі площин (П1П2) точок К (4; 2; 2), L (5; - 3; 4), М (6; -2; -3), N (1; 3; -5) і F (-2; 3; 4). Точки К і F належать першій квадранті, точка L – другій, точка М – третій, точка N – у четвертій квадранті. Надалі розглядаючи комплексне креслення фігур у системі площин (П1П2) приймається одиниця виміру – один міліметр і спеціально позначати штрихами не будемо.
Рис. 1.19
Креслення виробу обов’язково супроводжується параметризацією і нанесенням розмірів, за якими виготовляють виріб. При цьому система відліку, яку будемо називати натуральною системою координат, не співпадає із проекційною системою, проте її вибирають так, щоб її осі були відповідно паралельні осям проекцій (рис. 1.19).
Рис. 1.20
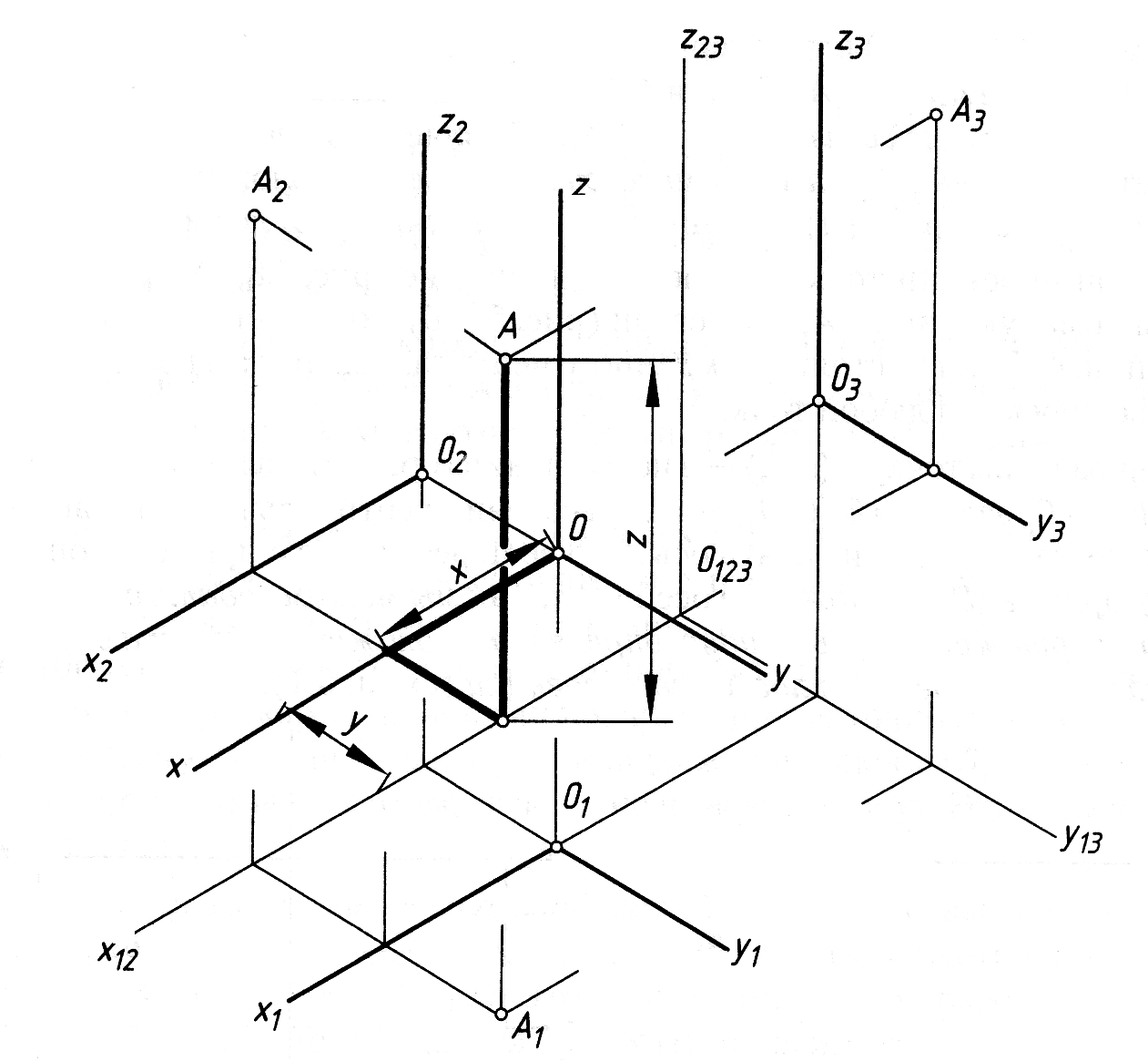
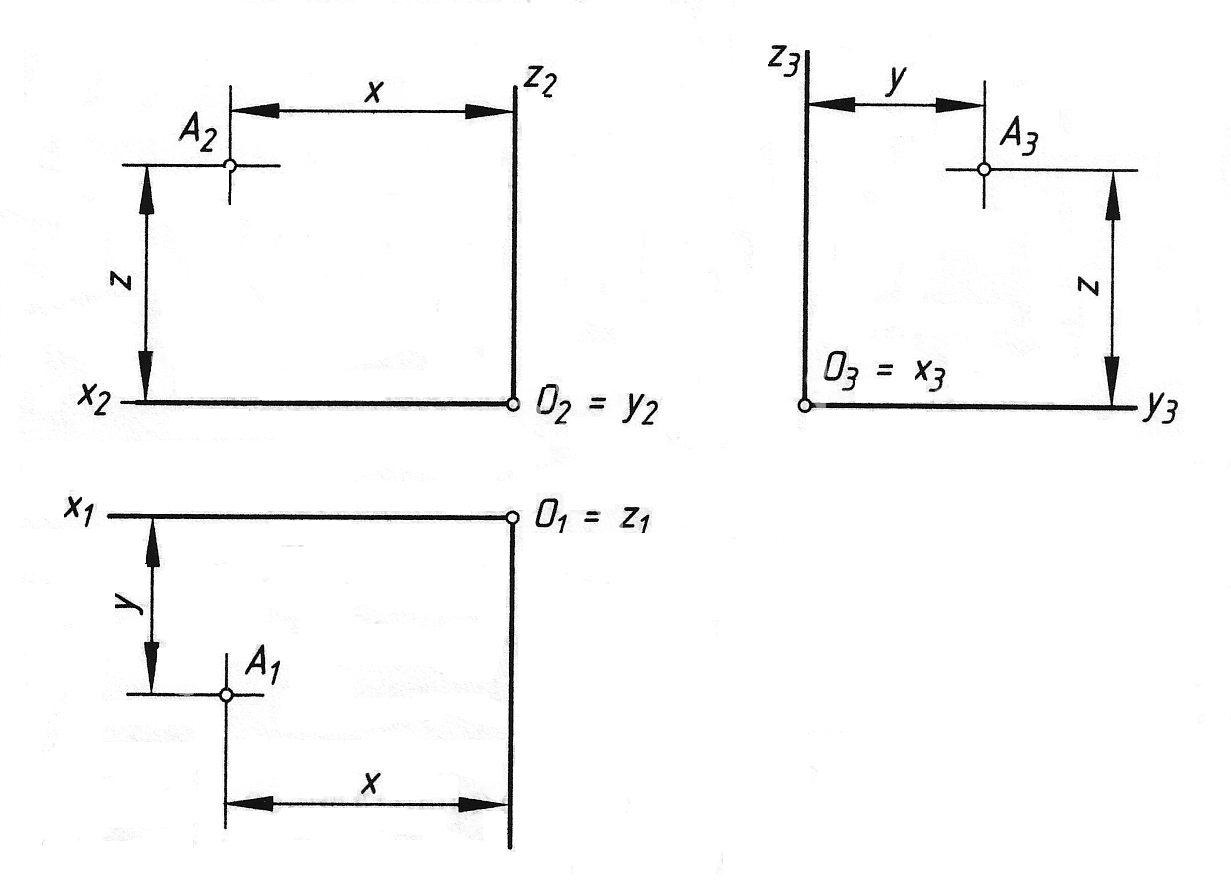
Натуральна система Охуz разом із об’єктом (точка А) спроеціюється на площину проекцій. При цьому її координатні площини паралельні площинам проекцій і їх поля перспективно відповідним. Для задання такої моделі на епюрі достатньо задати початок 0 (01 02 03) натуральної системи Охуz (рис. 1.20). Тоді зображення А1, А2, А3 об’єкту А можна побудувати за координатами А (хуz) натуральної системи.
Запитання і завдання для самоперевірки 1. У чому полягає суть центрального проеціювання? 2. У чому полягає суть паралельного проеціювання? 3. На які види поділяють паралельні проекції? 4. Як називають прямі А1А2, А2А3? 5. Що таке комплексне креслення точки і як його отримують? 6. У якій послідовності будують проекції точки за її координатами? 7. Що таке квадранти? Що таке октанти? 8. Якими способами можна побудувати третю проекцію точки за двома її відомими? 9. Які точки називаються конкуруючими? 10. Який октант симетричний першому відносно: горизонтальної площини проекцій; фронтальної площини проекцій; профільної площини проекцій; початку осей проекцій? 11. Які октанти розташовані над горизонтальною площиною проекцій; перед фронтальною площиною проекцій; праворуч від профільної площини проекцій? 12. По якій осі відкладають відстань від точки до: горизонтальної площини проекцій; фронтальної площини проекцій; профільної площини проекцій? 13. Чи можуть накладатись одна на одну дві, а той три проекції точки? Якщо так, то в якому випадку (дати пояснення)? 14. Чому одна проекція точки не визначає її положення у просторі? 15. Що таке натуральна система координат? 16. Побудуйте креслення точок, розташованих у різних октантах простору та встановіть їх положення: - точка А – Х≠0, Y≠0, Z=0; - точка В – Х≠0, Y=0, Z≠0; - точка С – Х=0, Y≠0, Z≠0; - точка D – Х≠0, Y=0, Z=0; - точка Е – Х=0, Y≠0, Z=0; - точка К – Х=0, Y=0, Z≠0.
Лекція № 2. Проекція прямої План: Пряма. Проекція відрізка прямої. Прямі часткового положення. Пряма загального положення. Знаходження натуральної величини відрізка прямої загального положення та кутів нахилу до відповідних площин проекцій. Сліди прямої. Точка на прямій. Взаємне положення прямих у просторі. Виклад основного матеріалу: Згадаємо вислів мудрих: «Пряма лінія в математиці (геометрії) так, як і в моралі, - найкоротший шлях» (Л.Еджворт). Поняття прямої лінії, очевидно, є абстракцією від натягнутої лляної нитки. Нитка була не тільки прообразом геометричної лінії, а й першим геометричним інструментом: натягнутий шнурок відігравав роль лінійки; закріплюючи один кінець шнурка, другим його кінцем як циркулем описували коло; поділяючи шнурок із зв’язаними кінцями на 12 рівних частин і надаючи йому форму трикутника, сторни якого відповідно дорівнюють 3, 4, 5 частина утворювали прямокутний трикутник; таким способом будували прямий кут. Греки називали староєгипетських геометрів, у яких вони навчалися геометрії – «натягувачами шнурків». Пряма – це безліч точок з одним виміром. З геометрії відомо, що пряма в просторі безмежна, а обмежену частину прямої називають відрізком. Таким чином, проеціювання прямої зводиться до побудови відрізка, який задано двома точками, наприклад, А і В. При ортогональному проеціюванні на площину пряма, не перпендикулярна до площини проекцій, проеціюється в пряму. Пряма в просторі відносно площин проекцій може займати різне положення: загальне або часткове. Пряму, яка не паралельна і не перпендикулярна жодній з площин проекцій, називають прямою загального положення. При цьому, жодна з проекцій не паралельна і не перпендикулярна до осей проекцій. Під час проеціювання прямої е на горизонтальну площину проекцій П1 отримаємо пряму е1, а під час проеціювання прямої е на фронтальну площину проекцій П2 – е2. Пряма е1 – горизонтальна проекція прямої е, пряма е2 – її фронтальна проекція (рис. 2.1). Пряму е називають прямою загального положення.
Рис. 2.1
На комплексному кресленні проекції прямої загального положення складають з осями проекцій довільні кути. Координати будь-якої точки прямої загального положення – мінливі величини: немає таких двох точок, для яких хоча б одна координата була однаковою. Оскільки положення прямої у просторі повністю визначають двома точками, то для визначення проекцій прямої досить визначити проекції будь-яких двох точок, які належать цій прямій. Провівши через точки А і В (рис. 2.2) перпендикуляри до площин проекцій П1 і П2, знайдемо проекції точок А і В: А(A1, А2), B(B1, B2).
Рис. 2.2 Рис. 2.3
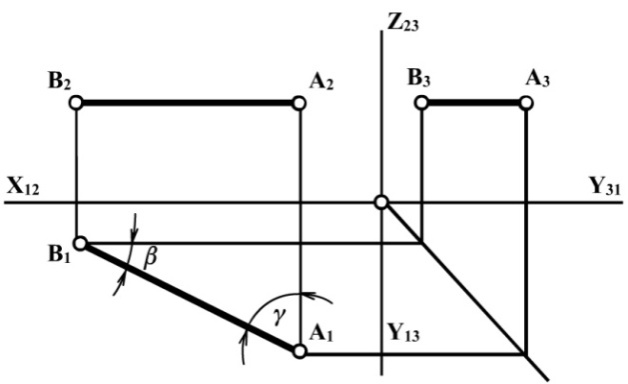
Для перетворення просторового макету відрізка АВ у плоске комплексне креслення, площину проекцій П1 необхідно повернути навколо осі Х12 на кут 900 за годинниковою стрілкою і провести перпендикуляри до осі Х12 з проекцій точок А і В – А1А2; B1B2 (вертикальні лінії зв'язку) (рис. 2.3). Відрізок АВ займає довільне положення щодо площин проекцій П1, П2, П3 (тобто кути нахилу відрізка АВ до П1, П2, П3 довільні, але відмінні від 0 і 900). Окрім розглянутого загального випадку розміщення прямої по відношенню до заданої системи площин проекцій, існують особливі (часткові) випадки: а) пряма паралельна до площини проекцій; б) пряма перпендикулярна до площини проекцій. Прямі, паралельні до площин проекцій, називаються лініями рівня. Горизонтальна пряма (горизонталь) – це пряма, паралельна до горизонтальної площини проекцій. Вона позначається буквою h(h1, h2, h3) (на рис. 2.4 відрізок АВ паралельний до П1). Усі точки горизонталі віддалені на однакові відстані від П1, тобто для усіх точок горизонталі координата Z – величина постійна (Z = const). А тому h2 || Х12 ( h2 Кут нахилу горизонталі до П1 – a = 0. Кут нахилу горизонталі до П2 – b і кут нахилу до П3 – g визначаються з горизонтальної проекції h – h1(А1 В1) (рис. 2.4). На площину проекцій П1 відрізки прямої h проеціюються в натуральну величину, а на дві інші площини – зі спотворенням – у вигляді відрізків меншої величини.
Рис. 2.4
Фронтальна пряма (фронталь) – це пряма, паралельна до фронтальної площини проекцій. Вона позначається буквою f(f1, f2, f3) (на рис. 2.5 відрізок СD паралельний до П2). Усі точки фронталі віддалені на однакові відстані від П2, тобто для усіх точок фронталі координата Y – величина постійна (Y = const). А тому f1 || Х12 ( f1 Кут нахилу фронталі до П2 – b = 0. Кут нахилу фронталі до П1 – a і кут нахилу до П3 – g визначаються з фронтальної проекції f – f2 (С2D2) (рис. 2.5). На площину П2 відрізки прямої fпроеціюються в натуральну величину, а на дві інші площини – зі спотворенням – у вигляді відрізків меншої величини.
Рис. 2.5 Рис. 2.6
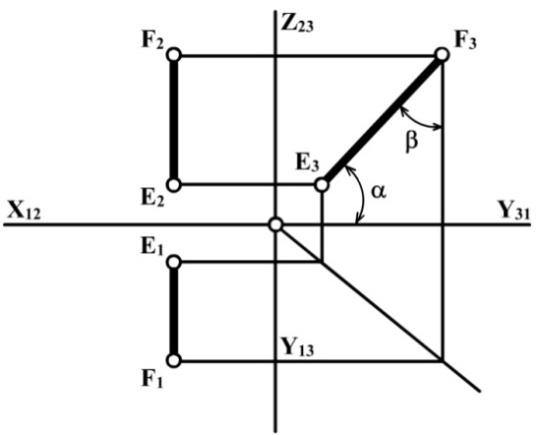
Профільна пряма – це пряма, паралельна до профільної площини проекцій. Вона позначається буквою р(р1, р2, р3) (на рис. 2.6 відрізок EF паралельний до П3). Усі точки профільної прямої віддалені на однакові відстані від П3, тобто для усіх точок профільної прямої координата Х – величина постійна (Х = const). А тому р1 Кут нахилу профільної прямої до П3 – g = 0. Кут нахилу профільної прямої до П1 – a і кут нахилу до П2 – b визначаються з профільної проекції р – р3 (Е3F3) (рис. 2.6). На профільну площину проекцій П3 відрізки прямої рпроеціюються в натуральну величину, а на дві інші площини – зі спотворенням – у вигляді відрізків меншої величини, які перпендикулярні осі Х12. Пряма може бути не тільки паралельною до площини проекцій, але і перпендикулярна ній. Проекціюючими називаються прямі які перпендикулярні до однієї з площин проекцій і паралельні двом іншим площинам проекцій (рис. 2.7).
Рис. 2.7
Пряма а ^ П1 – горизонтально проеціююча пряма; пряма b ^ П2 – фронтально проеціююча пряма; пряма c ^ П3 – профільно проеціююча пряма. На одній з площин проекцій проеціююча пряма зображується у вигляді точки, а на двох інших – у вигляді відрізків, які займають горизонтальне або вертикальне положення і величина яких дорівнює натуральній величині відрізка прямої.
|

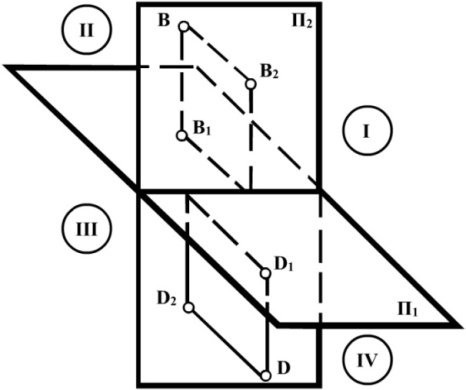 Площини проекцій П1 і П2 ділять простір на чотири двогранні кути, які називають квадрантами. Наприклад, точка В – ІІ квадрант; точка D – ІV квадрант (рис. 1.15).
Площини проекцій П1 і П2 ділять простір на чотири двогранні кути, які називають квадрантами. Наприклад, точка В – ІІ квадрант; точка D – ІV квадрант (рис. 1.15).


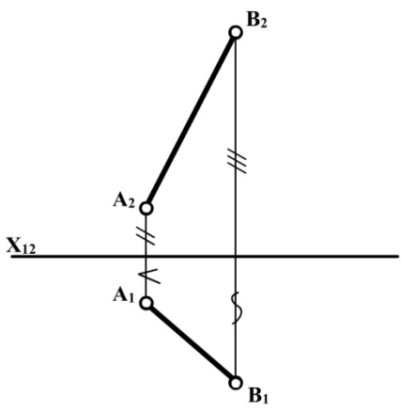 Відрізок А1В1 – горизонтальна проекція відрізка АВ, а відрізок А2В2 – його фронтальна проекція.
Відрізок А1В1 – горизонтальна проекція відрізка АВ, а відрізок А2В2 – його фронтальна проекція.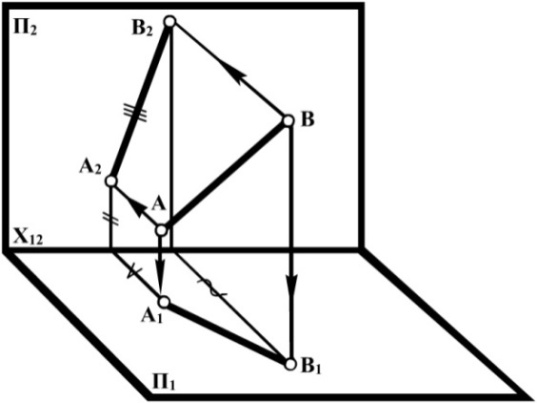
 Z23, h3
Z23, h3