Поділ відрізка у заданому відношенні

 

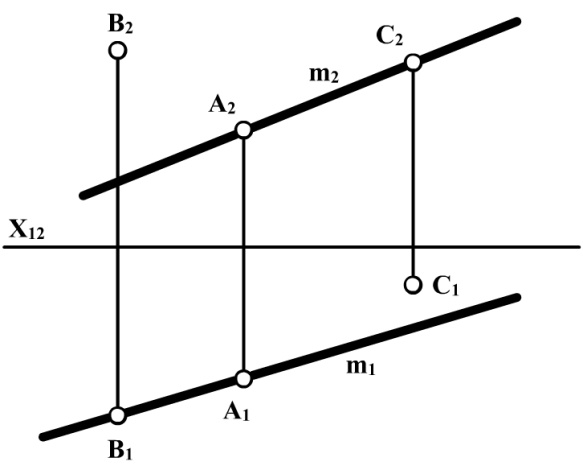
Якщо точка лежить на прямій, то її проекції лежать на однойменних проекціях цієї прямої і на спільній лінії зв’язку.

Точка А (рис. 2.8) лежить на прямій m, тому що її проекції А₁ і А₂ розташовані відповідно на горизонтальній m₁ і фронтальній m₂ проекціях прямої.

 

 

Рис. 2.8

 

Точки В і С не лежать на прямій m, тому що одна з проекцій кожної точки не належить проекції цієї прямої.

Точка, яка не лежить на прямій відносно прямої може займати різне положення. Наприклад: точка В знаходиться над прямою m, а точка С – за прямою m. Для визначення належності точки профільній прямій, необхідно побудувати профільні проекції точки та прямої.

Побудова відсутніх проекцій точок на прамій в окремих випадках вирішується просто, в інших випадках рішення неможливе, в третіх – рішення громіздке (табл. 2.1).

Таблиця 2.1

Належність точки прямій

Просто	Неможливо	Громіздко

 

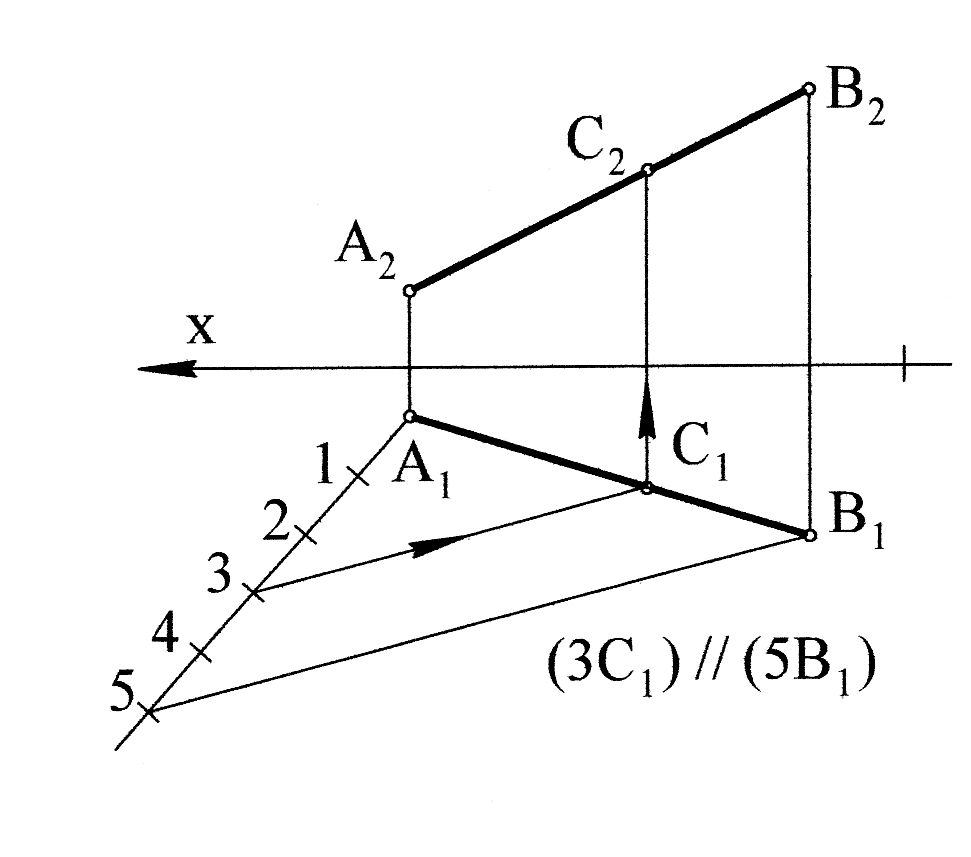
Розглянемо поділ відрізка АВ у заданному відношенні, наприклад 3:2. Згадаємо одну з властивостей паралельних проекцій: якщо точка ділить відрізок у даному відношенні, то проекція точки ділить проекцію відрізка у такому ж відношенні.

Щоб поділити відрізок АВ точкою С у відношенні 3:2 досить поділити одну його проекцію у даному відношенні (наприклад А₁В₁) відомим з геометрії способом. З точки А₁ проводимо довільний промінь, на якому від точки А₁ відкладаємо п’ять однакових довільних відрізків. Кінець п’ятого відрізка (точку 5) з'єднуємо з точкою В₁. Кінець другого відрізка позначаємо 3. Точка 3 ділить відрізок А₁5 у відношенні 3:2.

Рис. 2.9

 

Через точку 3 проводимо пряму, яка паралельна відрізку 5В₁. Ця лінія перетинає горизонтальну проекцію відрізка АВ в точці С₁. С₁ ділить А₁В₁ у відношенні 3:2. За допомогою лінії зв’язку знаходимо відсутню фронтальну проекцію точки С на А₂В₂ (рис. 2.9).