Взаємна перпендикулярність прямої і площини

 

Пряма перпендикулярна до площини, якщо вона перпендикулярна до двох прямих цієї площини, що перетинаються. Ця ознака перпендикулярності прямої і площини відома з геометрії.

Спочатку розглянемо часткові випадки, коли площина паралельна або перпендикулярна до площини проекцій.

 

Якщо площина паралельна площині проекцій, то пряма, яка перпендикулярна до неї, буде проеціюючою. Одна з її проекцій буде перпендикулярною до сліду проекції площини.

Наприклад, задано площину S || П₁ (рис. 3.23) і точку А(А_1,А₂). Необхідно через точку А провести пряму ί ^ S.

Оскільки S || П₁, а ί ^ S, то ί ^ П₁. А Î ί: ί ₁ º А₁, ί₂ ^ S₂.

 

Рис. 3.23 Рис. 3.24

 

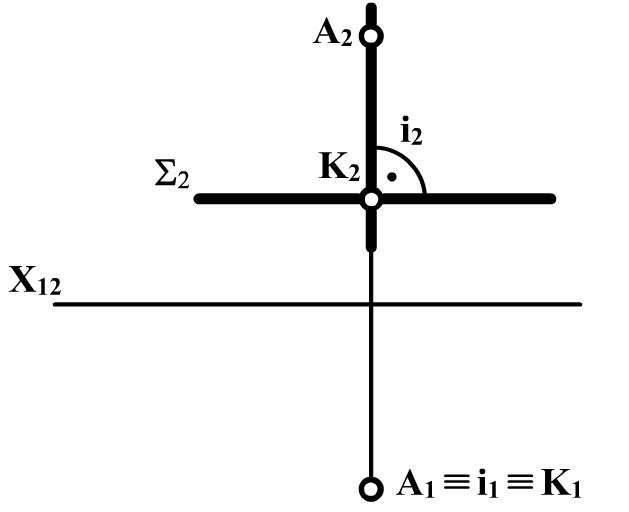
Якщо площина займає проеціююче положення, то пряма лінія, яка перпендикулярна до площини, буде прямою рівня.

Наприклад, задано площину S ^ П₂ (рис. 3.24) і точку А(А₁,А₂). Необхідно через точку А провести пряму l ^ S.

Оскільки площина S ^ П₂, а l ^ S, то пряма l || П₂ Þ l₁ || X₁₂,_, l₂ ^ S₂.

Якщо площина S займає загальне положення, то і перпендикуляр до цієї площини теж буде займати загальне положення.

На рис. 3.25 наведено приклади перпендикулярності прямої та площини (пряма та площина займає загальне положення та часткове).

Рис. 3.25

Висновок. Для того, щоб пряма у просторі була перпендикулярна до площини, необхідно і достатньо, щоб на комплексному кресленні горизонтальна проекція прямої була перпендикулярна до горизонтальної проекції горизонталі площини, а фронтальна проекція прямої перпендикулярна до фронтальної проекції фронталі площини (або необхідно і достатньо, щоб проекції цієї прямої були перпендикулярні до однойменних слідів площини): n₁^h₁, n₂ ^ f₂ Û n ^ S(f,h).

Можна провести перпендикуляр до площини з будь-якої точки, а потім розв'язувати задачу про знаходження точки перетину прямої з площиною. Розвиваючи цю думку, приходимо до задачі на визначення відстані від точки до площини. Визначимо відстань від точки А (A₁,A₂) до площини S (c || d) (рис. 3.26).

Рис. 3.26

 

Відстань від точки до площини вимірюється довжиною відрізка перпендикуляра, опущеного з точки на площину: n ^ S; A Î n.

1) Проводимо лінії рівня площини h і f.

2) Проводимо проекції перпендикуляра з точки А до площини S:

n₁ ^ h₁; n₂ ^ f₂. Зауважимо, що пряма n схрещується з f і h під прямими кутами, а тому основи перпендикуляра на площині ми не маємо.

3) Знаходимо точку К перетину прямої n з площиною S: К = n Ç S.

4) Визначаємо натуральну величину відрізка перпендикуляра АК способом прямокутного трикутника.